O anarquismo e o problema da escala
O problema da escala é talvez o problema mais fundamental do anarquismo.
Todos sabemos por experiência própria que o anarquismo funciona bem numa escala local. A maioria daqueles que têm sido activos no movimento anarquista têm também participado, pelo menos, nalgumas iniciativas como Food Not Bombs [Comida sim, Bombas não], infoquiosques [infoshops], pequenas editoras independentes, feiras do livro anarquistas, acções de entreajuda, Antifa, cooperativas de trabalhadores, socorristas de rua [street medics], transformatórios informáticos [hackerspaces] e transformatórios multiúsos [makerspaces], etc. O movimento anarquista tem uma vasta experiência histórica acumulada sobre como organizar tais iniciativas comunitárias locais. Não há dúvida de que o anarquismo funciona bem naquilo a que chamarei “a pequena escala”.
Historicamente, uma das principais críticas direccionadas contra o anarquismo tem sido a de que ele não oferece uma teoria convincente sobre como pode uma forma de organização descentralizada, não hierárquica, ser maximizada para funcionar eficientemente em “larga escala”. Essa objecção tem sido expressa frequentemente por militantes socialistas e comunistas que defendem formas de planeamento centradas em torno de uma estrutura partidária e/ou de uma organização estatal. É famoso o comentário de Leon Trotsky, na sua autobiografia, sobre como é que o seu entusiasmo inicial pelo anarquismo diminuiu quando os seus camaradas anarquistas foram incapazes de apresentar um bom plano para a administração do sistema ferroviário.
O comentário de Trotsky é insincero, mas a questão é legítima. Como é que o anarquismo lida com estruturas de larga escala? Existe uma boa estratégia de maximização para interpolar [*] o grande a partir do pequeno ? Embora seja certamente possível pensar em várias boas respostas para o problema específico da ferrovia, o problema mais geral da escala não é nada trivial: é bem conhecido o fato de que muitos sistemas físicos não podem ser maximizados livremente e deixam de funcionar fora de uma escala habitual de aplicabilidade. Seria o anarquismo um tal sistema, destinado a funcionar apenas na escala das pequenas comunidades locais?
Uma parte do movimento anarquista tem-se refugiado em tais posições “locais” e defendido o completo abandono do problema da escala, focando-se apenas na acção e na organização ao nível de pequenas comunidades. Eu considero que essa posição é incompatível com os ideais globais do anarquismo, cuja meta final é a libertação da humanidade (e de todas as entidades sencientes, biológicas ou mecânicas) da opressão e de estruturas hierárquicas de poder. Para atingir tais objetivos o anarquismo moderno tem de se comprometer com um mundo de alta complexidade e estruturas de larga escala dotadas de múltiplas camadas. Refugiar-se na zona de conforto de pequenas comunidades locais homogéneas vai à contracorrente da história das grandes aspirações e ideias revolucionárias e visionárias do anarquismo.
Existem outras tendências, bem diferentes, no interior do movimento anarquista, como o Left Market Anarchism, que não se esquiva de encarar o problema da escala, mas que defende, em essência, que ele seja resolvido tomando emprestado o mecanismo de mercado do capitalismo e “libertando-o”, de certa maneira, para que sirva a objetivos socioeconómicos mais justos e a uma sociedade mais igualitária. Considero essa abordagem pouco sedutora. Não acredito que os mercados possam ser “libertados” do capitalismo, nem que eles possam, enfim, fazer algo de bom, não obstante os seu estatuto de “libertado”. Isso porque, em essência, a meu ver, o mecanismo do mercado percorre uma rota descendente em direcção a um mínimo de custo/energia, num esforço para maximizar os lucros, inevitavelmente seleccionando as opções menos valiosas, ao mesmo tempo que descarta tudo o que possa ter algum valor (mas não possa gerar lucros) ao longo do processo. Chamem a isto o meu preconceito comunista.
Para os propósitos deste breve ensaio, pretendo analisar certos aspectos da questão da escala a partir de alguns pressupostos simplificadores que me inspiram confiança quando tento conceber a estrutura de uma sociedade anarquista (ou, pelo menos, de uma sociedade onde eu gostaria de viver). Assim, começarei por supor que o que acontece na “pequena escala” está estabelecido como uma rede de comunas, cooperativas e colectivos, geridos segundo formas anarco-comunistas de organização, e considerarei a questão de como introduzir estruturas de larga escala nessa rede.
O que quero dizer com “estruturas de larga escala” pode ser fundamentalmente descrito como “distribuição em larga escala de serviços”. Os serviços incluem todas as necessidades imediatas como transporte (a ferrovia anarquista!), saúde, produção e distribuição de conhecimento (conectividade, educação, circulação e acessibilidade da informação), a cadeia de distribuição de alimentos e insumos. Nada disso pode ser administrado estritamente ao nível de uma comunidade local, por mais bem planeada e eficiente que possa ser a produção de alimentos ou o transporte público local. Os serviços não são rentáveis, precisamente porque são serviços. A vantagem da sua existência é enorme, mas ela manifesta-se de formas indirectas que não resultam em lucro na prestação dos serviços em si. É por isso que é impossível esperar serviços de qualidade no capitalismo: o transporte baseado em automóveis é ineficiente e desastroso para o ambiente, o conhecimento é aprisionado por acessos pagos, a saúde é inacessível, a produção e a distribuição concentram-se no consumo acelerado de produtos de baixa qualidade, e assim por diante.
Por outro lado, um vasto e heterogéneo leque de posições políticas no interior do espectro socialista, desde as sociais-democracias até o autoritarismo estalinista, tem tradicionalmente investido o Estado da atribuição de assegurar a distribuição em larga escala de serviços. Essa convergência entre Estado e serviços tem o perigoso efeito de atrelar uma função útil (assegurar o acesso a serviços) aos mais desagradáveis e autoritários aspectos do Estado: uma grande fatia da produção é colocada ao serviço dos militares, a obediência é assegurada pela acção violenta da polícia, são abundantes as ineficiências e a centralização costuma tornar o planeamento ineficaz.
Analisarei brevemente algumas experiências, desenvolvidas historicamente no interior da perspectiva socialista/comunista, que visavam a descentralização e a dissociação entre serviços e poder estatal.
O comunismo e o problema da escala
Uma primeira observação que eu gostaria de fazer antes de continuar a discutir o problema da escala é que podemos facilmente virar a mesa no que diz respeito à “questão/objecção da escala”, que tem sido tratada historicamente como um problema do anarquismo, e formular a mesma questão como sendo um problema do comunismo. Supondo que à escala local o sistema económico comunista seja implementado eficientemente por meio de cooperativas de trabalhadores e comunas, como é que ele se maximiza para abarcar toda a cadeia de suprimentos e serviços de larga escala? Historicamente, o comunismo tem-se valido de economias centralmente planificadas, resultando muitas vezes em ineficiências desastrosas, combinadas com um autoritarismo opressivo. Contudo, muitas lições úteis e interessantes podem ser extraídas das várias tentativas malsucedidas de descentralização do planeamento económico comunista ao longo da história, e das dificuldades enfrentadas.
Nos tempos soviéticos, houve duas tentativas principais de utilizar métodos da computação para abordar o problema da escala na economia planificada. Uma foi a programação linear de Leonid Kantorovich [18], que, depois de uma fase inicial de forte obstrução pelas autoridades da época de Estaline, começou a ser admitida no final da década de 1950 [34]. As técnicas de programação linear foram depois adoptadas pelo planeamento económico soviético, começando pela cadeia produtiva das Forças Armadas nos anos 1960.

Embora os métodos de optimização de Kantorovich tenham sido explicitamente projectados para uma alocação eficiente de recursos numa economia comunista, a oposição extrema que enfrentaram na era estalinista deveu-se principalmente a semelhanças identificadas entre as “valorações” de Kantorovich e o sistema de definição de preços pelo mercado. Embora não seja este o principal assunto deste ensaio, gostaria de salientar que negar-se a tomar emprestados os mecanismos do capitalismo não implica (e não deveria implicar) uma rejeição cega da utilização de métodos de optimização matemática no contexto de uma economia comunista.
Mesmo num cenário de pós-escassez, com disponibilidade abundante de energia renovável, certos insumos continuariam escassos, simplesmente porque há uma distribuição desigual relativa de elementos químicos no universo. Evitar desperdícios e minimizar impactos ambientais continuariam a ser metas valiosas. Problemas de minimização podem ser, na verdade, bem resolvidos com o auxílio de técnicas como a programação linear, e não costumam suscitar divergências. São as metas de maximização que representam a parte mais difícil do nosso problema da escala.
A questão não é a de saber se métodos de optimização são úteis em si, mas antes o que é que está a ser optimizado. O problema principal, ao qual retornarei mais adiante, é que, quando se trata da distribuição de serviços em larga escala numa economia comunista, exige-se um nível muito mais elevado de complexidade informacional para a projecção de um sistema válido de valorações e constrições, um sistema que não reflicta a noção capitalista simplista de lucro, mas que possa captar vantagens que se manifestam apenas numa escala espácio-temporal muito maior e em níveis de complexidade muito profundos. A abordagem de Kantorovich à programação linear também sofre, em princípio, com o problema da escala, já que as valorações não são independentes da escala, e a dependência relativamente à escala — da complexidade necessária para encontrar um bom sistema de valorações e constrições — é uma parte crucial do problema. A aposta dos mercados na optimização dos lucros desvia do problema, a ponto de inviabilizar a solução.
A outra tentativa histórica de introduzir métodos da computação para abordar o problema da escala numa economia comunista, geralmente menos conhecida, mas mais interessante para o objetivo da nossa discussão, foi o projeto cibernético de Victor Glushkov, de uma rede descentralizada de retroalimentações de mecanismos computacionais, baseado numa forma rudimentar de inteligência artificial. Nesse plano, uma vasta rede de computadores inteiramente descentralizada teria eventualmente despojado o Estado das atribuições do planeamento económico e da distribuição de serviços. Desnecessário dizer que o projecto foi veementemente combatido pelo governo soviético, depois de uma fase inicial de breve entusiasmo se evaporar rapidamente. Um relato pormenorizado da história desse projecto está disponível em [28], ao passo que uma contextualização mais geral do papel da cibernética na União Soviética é discutida com profundidade em [13].
A história do comunismo cibernético
Nos primórdios da Revolução Russa, um precursor significativo da cibernética foi proposto na “Tectologia” do dirigente bolchevique transhumanista Aleksandr Bogdanov [14] [21].

Entretanto, quando Norbert Wiener introduziu a nova ciência da cibernética em 1948 [35], ele foi atacado e condenado pelo regime de Estaline, como em vários outros campos da ciência contemporânea, exceptuando aquilo que se tornou imediatamente necessário para o desenvolvimento de armas nucleares [16] [29].

Apesar da proibição oficial, o interesse na cibernética começou a crescer entre os cientistas soviéticos, graças principalmente aos seminários particulares do matemático Aleksei Lyapunov [13]. A reabilitação oficial da cibernética começou apenas depois de 1953, o ano da morte de Estaline, com um famoso artigo de Anatoly Kitov, Aleksei Lyapunov e Sergei Sobolev (todos pesos-pesados da organização oficial soviética da ciência) [19]. Por volta de 1967, a cibernética na União Soviética contava com quinhentas instituições de investigação e dezenas de milhares de investigadores [13][28].
As reformas económicas tornaram-se uma necessidade premente na metade dos anos 1950, depois de o regime de Estaline ter deixado o país em grandes dificuldades, a cadeia de abastecimento e o sector agrícola à beira do colapso, e o sério risco de outra grande fome à espreita. No meio de uma rápida expansão do sector técnico-científico, dos êxitos iniciais do programa espacial soviético aos primeiros grandes avanços nos sistemas de computação e automação, várias propostas concorrentes de reforma económica promoviam a ideia de uma “solução computacional” para os graves problemas de gestão da economia planificada.
Foi nesse cenário que o matemático Victor Glushkov concebeu um grande plano para livrar a economia comunista do planeamento central do governo soviético, substituindo-o inteiramente por uma rede autónoma e descentralizada de computadores.

Esse maciço projeto, o OGAS (Sistema Nacional Automatizado para a Computação e Processamento de Informação), foi apresentado directamente a Khrushchev em 1962, tendo sua fase inicial sido autorizada em 1963. O projecto original desse sistema descentralizado de computação remota foi pensado para os trabalhadores, era antiburocrático e não hierárquico [28].
Nessa visão da cibernética, o conceito de heterarquia de McCulloch’s [26] possibilitava o desenvolvimento de sistemas complexos fora da lógica restritiva de uma dicotomia entre hierarquia e mercados estáveis, enfatizando, em vez disso, a auto-organização, ciclos de retroalimentação e redes complexas [28].
O plano original, nessa abordagem cibernética, era o de implementar um sistema de computação descentralizado, capaz de processar retroalimentações em tempo real e lidar com a simulação de dinâmicas complexas. Para fornecer um modelo computacional maximizável, os projectistas focaram-se principalmente na programação linear de Kantorovich, que parecia a ferramenta matemática mais promissora da época. Como mencionámos, a escalabilidade das valorações de Kantorovich é subtil, e discutiremos uma abordagem mais moderna para a escalabilidade na próxima secção deste artigo. No entanto, o aspecto mais importante da proposta era a noção de uma rede cibernética computacional e do seu papel na implementação de um mecanismo descentralizado e autónomo de computação para o sistema económico comunista que não precisaria de um planeamento centralizado.
Tornou-se rapidamente evidente que os custos previstos para a implementação desse projeto em todo o território soviético seriam enormes, mas ficou ainda mais claro que a meta de substituição do planeamento central e seu controlo pelo governo soviético, por um sistema computacional descentralizado, autónomo e não hierárquico, era uma ameaça direta ao poder instalado. Por volta da época da transição entre os governos Khrushchev e Brezhnev (1964-1965), o governo soviético optou, em vez disso, pelas propostas muito menos ameaçadoras das reformas económicas de Kosygin-Liberman. Estas baseavam-se no plano económico de Evsei Liberman [22] [24], focado na introdução de medidas para a obtenção de lucros e de um mecanismo de mercado. Assim, a dinâmica menos custosa e ameaçadora de mercados voltados para o lucro pôs fim, efectivamente, ao plano muito mais interessante e potencialmente revolucionário de um grande sistema cibernético descentralizado e autónomo que não se baseava no mecanismo do lucro. A própria reforma Kosygin-Liberman foi eventualmente abandonada em 1970 [28].
O comunismo cibernético não foi retomado na União Soviética, ainda que a cibernética continuasse a desfrutar de uma popularidade generalizada na cultura soviética nos anos 70. Contudo, outra experiência de comunismo cibernético desenvolveu-se de maneira independente no Chile de Allende. Ela estava quase pronta no início dos anos 1970, mas permaneceu inacabada quando o governo Allende foi violentamente derrubado pelo golpe fascista de Pinochet [27].
Ao contrário do governo soviético, que travou rapidamente o projecto OGAS quando percebeu que ele representava uma ameaça à sua chefia autoritária, Allende estava genuinamente aberto à ideia de um comunismo descentralizado e não autoritário, abraçando entusiasticamente a ideia de uma solução cibernética. Em 1971, o governo Allende contactou o socialista britânico e ciberneticista Stafford Beer, pedindo-lhe auxílio para a implementação de um sistema de apoio descentralizado, para a gestão da economia nacional, que respeitasse a autonomia dos trabalhadores e evitasse a imposição de uma cadeia de comando hierarquizada.

Beer aceitou entusiasticamente a tarefa e tornou-se o principal arquitecto do Projeto Cybersyn, que consistia numa vasta rede de colecta de dados por máquinas telex, um programa informático de modelos estatísticos, um programa informático de simulação económica e uma sala de operações onde observadores humanos poderiam supervisionar o fluxo de dados e os resultados dos modelos, e reagir a possíveis emergências. A principal meta de Beer era desenvolver fábricas autorreguladas e atribuir o poder de decisão inteiramente a estruturas controladas pelos trabalhadores, de uma tal maneira que se tornassem compatíveis (através do sistema computacional) com uma economia nacional de larga escala. Embora o Cybersyn tenha estado muito mais perto de ficar plenamente funcional do que seu equivalente soviético, o fim trágico e súbito de Allende e a queda do Chile nas trevas da tirania fascista liquidaram completamente a possibilidade de vê-la em prática. Quando os militares tomaram de assalto o palácio presidencial, destruíram a sala de operações do Cybersyn e desmantelaram o sistema por completo [27].
O comunismo requer complexidade
Antes de passar à apresentação de uma proposta mais concreta para a resolução do problema da escala, gostaria de sublinhar que só é possível maximizar um modelo de organização e produção baseado em princípios anarco-comunistas se houver capacidade suficiente de processamento de informações complexas.
A título de referência, remeto o leitor para um estudo recente [31], onde dados históricos (do Seshat Global History Databank) de uma grande variedade de sociedades, de aldeias a impérios, são analisados. O método da Análise de Componentes Principais (ACP) foi aplicado aos dados, permitindo que fossem mapeados num espaço bidimensional definido pelos dois primeiros componentes principais, englobando a maior parte das variações nos dados. Visualizados desse modo, os dados obedecem a um padrão altamente estruturado. Observando as variações no segundo componente principal causadas pelo aumento dos valores no primeiro, sociedades mais antigas mostram uma fase inicial muito concentrada, que pode ser interpretada como um aumento da escala acompanhado por um baixo crescimento relativo da capacidade de informação. Em seguida, observa-se um limiar (que os autores chamam de “limiar de escala”) depois do qual o padrão das sociedades que crescem em escala, mas não em complexidade informacional, começa a divergir significativamente do padrão daquelas sociedades cuja capacidade informacional alcançou um crescimento mais significativo.
Um segundo limiar (o “limiar de informação”) possibilita um aumento de escala naquelas sociedades que alcançaram um nível suficientemente elevado de capacidade de processamento de informações. Há uma área nesse espaço bidimensional de parametrização onde as sociedades ficam mais dispersas, indicando diferentes padrões possíveis de desenvolvimento nesse quadro de escala/informação. Quando o segundo limiar é ultrapassado, volta a predominar o aumento da escala e as sociedades tendem a concentrar-se novamente nesse espaço de parametrização, exibindo traços menos diversificados. A base de dados usada nesse estudo foi elaborada para a análise de sociedades pré-modernas, daí que, como advertem os autores, o comportamento dessas sociedades pareça ser artificialmente homogéneo depois de terem ultrapassado o limiar da informação, devido à saturação de muitas das variáveis à medida que dados sobre sociedades mais modernas vão sendo encontrados.
O socialismo e o comunismo são fenómenos intrinsecamente modernos, exigindo sociedades industriais e da informação (os primitivistas que se danem). Mesmo assim, podemos fazer algumas observações úteis a partir da análise realizada em [31]. Em particular, quando diferentes formas de organização se manifestam em sociedades de pequena escala, o desenvolvimento social, se a escala aumentar significativamente, mas for restringida por uma capacidade relativamente baixa de processamento de informações, tende a dar origem a formas autoritárias de Estado. A desigualdade económica costuma aumentar rapidamente nessa fase. Só quando uma complexidade informacional suficiente é alcançada é que diferentes formas de desenvolvimento se tornam novamente possíveis.
Deixando momentaneamente de lado a questão da validade dos dados do Seshat para sociedades mais modernas, podemos interpretar a enfâse renovada no aumento da escala (em vez de um crescimento contínuo da complexidade informacional) depois da transição da segunda fase como um aspecto das sociedades capitalistas modernas. Isso sugere que devemos esperar outra fase de transição — para um crescimento significativo da capacidade de gestão da informação — para que novas formas de organização não capitalistas se tornem possíveis na escala actual das sociedades contemporâneas. Por outras palavras, é necessário um aumento significativo da complexidade informacional para tornar possível um comunismo não autoritário. Por outro lado, o fascismo pode ser entendido como a tentativa de obter um aumento na escala (aspirações imperiais) combinada com uma dramática supressão de todos os níveis de complexidade.
Historicamente, as sociedades que tentaram implementar um modo comunista de produção, na ausência de um nível suficiente de complexidade informacional, acabaram por apostar no planeamento central e regredir para formas políticas autoritárias. Apesar da experiência histórica, muitas forças políticas, da social-democracia tradicional, passando pelo eurocomunismo do pós-guerra (como o PCI italiano), ao actual socialismo democrático, continuam a defender que podem existir soluções estatistas sob formas não autoritárias para o problema da distribuição em larga escala de serviços no socialismo. No entanto, tais soluções continuariam a depender de formas de coerção (tributação, força policial) para levar a cabo a expropriação e distribuição da riqueza. Pouco importa que tais formas de coerção sejam apresentadas como benignas; a longo prazo, o facto de um sistema de trabalho depender da ameaça do uso da força para se manter em funcionamento torna-o intrinsecamente frágil.
Em última análise, tanto a rede cibernética de Victor Glushkov, que não chegou a ser implementada na União Soviética, como o sistema Cybersyn de Stafford Beer, que ficou inacabado no Chile de Allende, foram tentativas de incrementar drasticamente a capacidade de processamento de informações complexas nas suas respectivas sociedades, como uma condição necessária para a existência de um comunismo descentralizado e não autoritário capaz de se maximizar para alcançar o nível das grandes redes.
A objecção comunista aos mercados
Gostaria de reiterar que minha objeção comunista aos mercados é que uma matemática melhor e mais sofisticada do que aquela que costuma ser aplicada quando pedimos emprestados os mecanismos do capitalismo é necessária para formular e enfrentar o problema da escala numa economia comunista, numa perspectiva descentralizada e não autoritária, Basear-se em métodos matemáticos inadequados resultará em soluções ineficazes e indesejáveis. O capitalismo e os seus desastres podem cavalgar a onda de um simples processo de optimização baseado no lucro, à custa de uma devastação generalizada, mas isso não é algo que devamos tentar emular. Se um problema é, ao mesmo tempo, difícil e suficientemente interessante para merecer o desenvolvimento inovador de um aparelho teórico apropriado, então isso é “Algo que precisa de ser feito”, sem pactuar com dúbios atalhos capitalistas.
Acho que este esclarecimento é necessário porque há uma tendência generalizada para conceber a objecção comunista aos mercados em termos de uma objecção absoluta ao uso de métodos matemáticos de optimização e análise. Gostaria de poder reduzir essa tendência a um efeito colateral do estado deplorável do comunismo na América do Norte. Contudo, figuras proeminentes da tradição comunista europeia não autoritária (como a dos Autonomistas) têm apoiado esse ponto de vista recentemente, como se pode ver, por exemplo, em textos recentes de Bifo [5] [6]. Por exemplo, lemos em [5] que “podemos afirmar que desvencilhar a vida social da dominação selvagem da exatidão matemática é uma missão poética, pois a poesia é a linguagem do excesso” e lemos em [6] que “o poder baseia-se hoje em relações abstratas entre entidades numéricas […] Não há escapatória política dessa armadilha: apenas a poesia, enquanto excesso do intercâmbio semiótico, é capaz de reanimar a vida”. Apesar do que sugerem Bifo e outros, não há qualquer identidade entre a abstracção matemática e o capitalismo financeiro, constrastada com uma oposição poética à abstracção. Expressa nesses termos, a objecção não faz qualquer sentido, não só porque a poesia é intrinsecamente uma forma de abstracção e a matemática é, em grande medida, um tipo de imaginação poética, mas porque é precisamente a nossa capacidade de imaginação poética matemática que nos permitirá conceber uma alternativa viável ao mundo do capitalismo e das finanças.
Como foi discutido acima, no que toca ao episódio da programação linear de Kantorovich, a oposição cega aos modelos matemáticos é uma reacção genuinamente estalinista, não um ponto de vista que o anarco-comunismo deva adoptar. O comunismo é essencialmente tecno-optimista: isso é algo que certas tendências primitivistas anticivilizacionais do anarquismo podem ter dificuldade de digerir, mas é inerente à natureza tanto do socialismo quanto do comunismo que a expropriação dos meios de produção requer a existência de meios de produção suficientemente sofisticados, que compensem a expropriação. Procurar abordar problemas cruciais como a distribuição de recursos e serviços numa economia comunista através de uma análise matemática e científica cuidadosa é a abordagem natural do comunismo. Digamo-lo mais uma vez, se não fosse o facto da actual cena comunista (e anarco-comunista) ter desenvolvido uma visão tão distorcida da ciência e da tecnologia, seria absolutamente desnecessário esclarecer o que é auto-evidente.
O processo de maximização dos mercados, voltado para o lucro, não é uma opção viável, não porque “lucro” seja uma palavra detestável (que é !) mas pelo modo como funciona a sua dinâmica: mesmo que pudéssemos partir de um cenário inicial ideal de riqueza distribuída igualitariamente, pequenas flutuações seriam radicalmente maximizadas, reproduzindo rapidamente um cenário de acumulação desigual. Na dinâmica de lucro dos mercados, a distribuição equitativa da riqueza é uma condição necessariamente instável. É por isso, em essência, que os mercados não podem ser libertados do capitalismo. Os mercados são causadores automáticos de desigualdades, que podem acabar rapidamente com quaisquer ganhos duramente conquistados, ao custo de graves convulsões sociais e acções revolucionárias difíceis de realizar. (Todos queremos uma Revolução, mas não uma que vá imediatamente por água abaixo se alguém activar a máquina de restauração acelerada do capitalismo comummente conhecida como mercado!) Para impedir que as disparidades na acumulação da riqueza sejam inexoravelmente restauradas, é preciso desenvolver um processo de optimização completamente diferente, não baseado no mecanismo de maximização de lucros do mercado.
Farei uma comparação metafórica para explicar melhor este ponto de vista. Quando, na história moderna da física, os fenómenos quânticos exigiram uma compreensão teórica adequada, os físicos empregaram métodos já conhecidos e que já estavam disponíveis, como a álgebra linear e as equações lineares parciais diferenciais. Isso não significa que a adaptação imediata de modelos matemáticos desenvolvidos para descrever fenómenos da física clássica tenha disponibilizada um modelo capaz de resolver os problemas da mecânica quântica. O malogro da teoria das “variáveis ocultas” mostrou que a aplicação de modelos da física clássica a fenómenos quânticos é, na verdade, simplesmente impossível. Pelo contrário, uma teoria matemática completamente nova, baseada nos espaços de Hilbert e nos operadores lineares, teve de ser desenvolvida para descrever os fenómenos quânticos.
Quando digo que é preciso desenvolver um modelo matemático apropriado para a resolução do problema da escala numa perspectiva anarco-comunista, não quero dizer que os métodos existentes não possam ser usados como alicerces ou níveis intermediários. Como demonstrarei na secção a seguir, há muitas teorias disponíveis que serão úteis e que deveriam ser aproveitadas. O que estou a dizer é que o que devemos almejar é algo semelhante ao desenvolvimento de uma teoria matemática para uma descrição preditiva dos fenómenos quânticos: modelos já existentes não teriam viabilizado uma solução, nem todo o edifício teórico que precisava ser construído, não obstante alguns dos seus alicerces fundamentais já estarem disponíveis nas teorias previamente existentes.
A auto-organização em redes e o problema da escala no anarquismo
Não vou tentar apresentar uma solução definitiva para o problema da escala no anarquismo, mas esclarecer aspectos importantes que nos podem levar, espero, a uma formulação mais precisa do problema. Esta secção será um pouco mais técnica, na medida em que analisarei alguns métodos de análise de redes complexas, que acho que devem ser encarados como ferramentas necessárias para abordar o problema da escala numa perspectiva anarquista.
Uma premissa fundamental, para formualar mais precisamente o problema da escala no anarquismo, é que o anarquismo é essencialmente um processo de auto-organização em redes complexas. O fenómeno da auto-organização em redes é amplamente estudado na teoria dos sistemas complexos, impulsionada por um conjunto de modelos, dos sistemas de telecomunicações à neurociência. Contudo, o que precisamos desenvolver vai além de uma reformulação ou de uma aplicação directa desses modelos. O que eu gostaria de esboçar aqui é uma breve síntese daquilo que considero serem os aspectos mais complicados e cruciais do problema.
Ludwig von Mises, no seu conhecido ensaio de 1920, em defesa dos mercados contra a tendência então em rápido desenvolvimento rumo ao planeamento económico socialista, procurava apresentá-los como um dispositivo computacional eficiente. Como foi discutido num ensaio introdutório em [9], “A provocação que Mises fazia ao socialismo era decididamente tecnocrática: apresentar uma infraestrutura computacional alternativa que pudesse competir com o sistema de preços […] Foi uma provocação da qual poucos socialistas conseguiram esquivar-se, e ainda menos foram os que conseguiram enfrentá-la”.
A lacuna no desenvolvimento de uma tal “infraestrutura socialista alternativa de computação” é realmente lamentável. Contudo, para sermos honestos, é bem possível que a matemática necessária para apresentar uma resposta socialista/comunista viável para a provocação de Mises simplesmente não estivesse disponível à época, e por muito tempo depois dela. Mesmo aquando das tentativas de implementar formas de comunismo cibernético, nos anos 60 e no início dos anos 70, a teoria das redes complexas estava ainda na infância. É provável que, embora tivessem a ideia geral correcta na cabeça, os esforços de Victor Glushkov e Stafford Beer falhassem ao serem implementados nas condições científicas e tecnológicas da época, simplesmente porque a capacidade de processamento de informações era ainda muito baixa e alguns instrumentos matemáticos cruciais não estavam ainda à disposição. Estamos hoje numa posição muito melhor para apresentar uma alternativa viável aos mercados, portanto não há mais desculpas para fugir do problema.
O que vou escrever nesta secção deve ser entendido como um exercício ao estilo das “Economic Science Fictions”, como aqueles discutidos com profundidade em [9], e como um exercício de imaginação matemática, como mencionámos acima. O objectivo é conceber a forma matemática de uma infraestrutura comunista cibernética de computação capaz de substituir o mecanismo de optimização de lucros dos mercados.
Complexidade
Antes de mais nada, a complexidade é aqui a noção fundamental, mas é também uma noção muito subtil, difícil de precisar. A principal definição de complexidade na matemática é a complexidade de Kolmogorov, que define a complexidade de alguma coisa como o tamanho do menor processo (algoritmo) que a realiza [23]. Nomeadamente,
(1)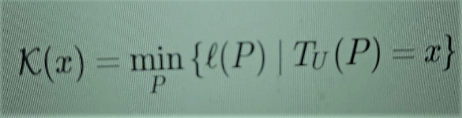
o que significa que a complexidade de x é o tamanho mínimo ℓ(P) de todos os programas P que, executados num computador universal TU (máquina de Turing), produzirão o resultado x. Faço esse esclarecimento porque facilita a comparação com outras definições, e porque também farei menções à “complexidade relativa”, à qual regressarei mais adiante. Ela é dada por meio de
(2)
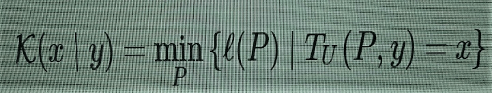
que é a mesma coisa, porém o computador TU é autorizado a usar a entrada y além do programa P para computar x.
A complexidade de Kolmogorov é ela própria uma função não-computável, porque o “problema da paragem”, que determina se um programa continuará a correr para sempre ou parará a certa altura, com determinado resultado, é em si mesmo um problema indecidível. Surpreendentemente, a não computabilidade em si não é um obstáculo sério porque a complexidade de Kolmogorov possui vários limites superiores perfeitamente computáveis (por qualquer algoritmo de compressão), o que significa que não pode ser calculada, mas pode ser estimada por excesso, de maneira computável. Há, no entanto, outra desvantagem mais séria no uso da complexidade de Kolmogorov: ela não corresponde à noção intuitiva de complexidade que desejamos modelar, visto que, embora atribua correctamente uma baixa complexidade a padrões facilmente previsíveis, confere, por outro lado, uma complexidade máxima a padrões completamente aleatórios. Maximizar a aleatoriedade não é, claro, o resultado desejado, independentemente da concepção ingénua e errada de anarquismo que circula entre os liberais. A entropia de Shannon assemelha-se a uma versão de valor médio da complexidade de Kolmogorov,
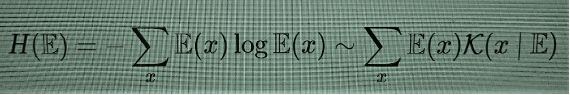
e tem a mesma tendência para detectar aleatoriedades, portanto, em si mesma, também não ajuda.
Existem formas de conceber medidas de complexidade mais voltadas para detectar a “complexidade estruturada”, em vez da complexidade oriunda da imprevisibilidade da aleatoriedade. Uma primeira modificação possível na complexidade de Kolmogorov, capaz de captar melhor uma forma de “complexidade organizada”, é dada pela profundidade lógica. Essa noção foi introduzida em [3], usando o tempo de execução de um programa quase mínimo em vez do tamanho do programa mínimo, como no caso de Kolmogorov. Ou seja,
(3)
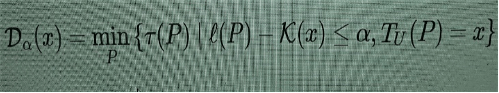
o que significa computar o tempo mínimo de execução de um programa P que gera x, cujo tamanho é igual ou apenas um pouco maior que o mínimo (cujo tamanho é K(x)). A discrepância permitida entre o tamanho mínimo K(x) e ℓ(P) é medida por um parâmetro variável α. (Mais precisamente, usa-se uma forma ligeiramente diferente da complexidade Kolmogorov K(x) em (3), mas não vou entrar em pormenores aqui: eles podem ser encontrados em [2].) Passar do mínimo para o quase mínimo serve para evitar que alguns programas um pouco maiores possam ter um tempo de execução menor. Mais interessante ainda, passar do tamanho de um programa para seu tempo de execução pode parecer, a princípio, uma mudança ínfima, já que o tempo de execução pode ser visto como uma outra modalidade de tamanho (no tempo, não na memória), mas produz um efeito significativo na redução do papel da aleatoriedade em padrões de alta complexidade. Uma análise comparativa da complexidade de Kolmogorov e da profundidade lógica pode ser encontrada em [10]. A razão pela qual não quero usar esta simples modificação da complexidade de Kolmogorov reside num fenómeno da “transição de fase” descrito em [2], que mencionarei em seguida, o que dificulta o uso da profundidade lógica como base para a construção de uma função de optimização.
Murray Gell-Mann propôs uma noção de “complexidade efectiva” e uma noção de “complexidade potencial” [11], com o objetivo de captar mais adequadamente a nossa noção intuitiva da complexidade como um fenómeno altamente estruturado. A complexidade efectiva serve para obter o conteúdo de informação das “regularidades” de um padrão, enquanto a complexidade potencial é uma noção semelhante que serve para incorporar as mudanças no tempo. Uma primeira descrição matemática da complexidade efectiva foi apresentada em [12]. Infelizmente, nenhuma dessas noções possui ainda um formalismo matemático completamente bem desenvolvido. Podemos, no entanto, partir do estádio actual, no que diz respeito às noções mais promissoras de complexidade, e ver o que podemos fazer com elas.
Uma boa síntese sobre o atual estádio dessas medidas de complexidade encontra-se em [2], a que me referirei na súmula que aqui estou a fazer. Para obter uma descrição apropriada da complexidade efectiva, consideremos uma combinação entre a complexidade de Kolmogorov e a entropia de Shannon, denominada “informação total” K(E)+H(E). Ela pode ser descrita como a complexidade algorítmica de x (a parte de Kolmorogorov K(x∣E)) ao computarmos o conjunto estatístico E ao qual x pertence (a parte de Shannon H(E)). O melhor conjunto estatístico E para um dado x é aquele que minimiza a informação total, o que é uma outra maneira de dizer que se trata da explicação mais provável para um dado x. Tendo sido seleccionado o modelo estatístico adequado E, podemos detectar se o elemento x é “típico” nesse conjunto estatístico, verificando se a probabilidade E(x) não é muito menor do que o tamanho médio 2−H(E), previsto pela entropia de Shannon. Dado x, é possível seleccionar, assim, o conjunto Mx de todos os conjuntos estatísticos possíveis E com pequena informação total e para o qual x é típico (possivelmente com restrições adicionais no que se refere ao conjunto de “boas teorias” que pretendemos considerar). A “complexidade efectiva” ε(x) é o valor mínimo da complexidade de Kolmogorov K(E) entre todos os conjuntos concorrentes E,
(4)

Observe-se que estamos aqui a definir complexidade efectiva como sendo um mínimo de complexidade de Kolmogorov em relação a um certo conjunto de modelos estatísticos E que explica um certo dado x, o que significa que queremos selecionar a explicação mais simples, de um conjunto de teorias plausíveis. Isso parece contradizer o que mencionei anteriormente, a saber, que procuramos uma maximização da complexidade informacional. No entanto, essa maximização ainda está por vir: a minimização que acabei de descrever é simplesmente uma fase preliminar necessária que atribui um valor de complexidade apropriado a um dado.
O que ganhamos usando a complexidade efectiva ε(x) em vez da complexidade de Kolmogorov K(x) ou da entropia de Shannon H(E)? A principal vantagem é que agora padrões completamente aleatórios têm uma pequena complexidade efectiva! Portanto, objectos com grande complexidade efectiva são gerados por “complexidade estruturada”, e não por aleatoriedade. Não é imediatamente óbvio que a complexidade efectiva de padrões aleatórios seja pequena: uma prova desse facto é dada, por exemplo, no Teorema 10 de [2], enquanto alguns casos de padrões não aleatórios que exibem grande complexidade efetiva são descritos no Teorema 14 de [2].
O fenómeno de “transição de fase” mencionado acima para o comportamento da profundidade lógica é baseado em como Dα(x) muda em comparação com a complexidade efectiva ε(x) . É possível demonstrar (veja o Teorema 18 de [2] para mais pormenores) que, para pequenos valores de ε(x), a complexidade lógica também pode assumir pequenos valores, mas quando a complexidade efectiva ultrapassa um valor limite (que depende da complexidade de Kolmogorov), a profundidade lógica salta repentinamente para valores muito grandes. Essa transição de fase repentina no comportamento de Dα(x) torna seu uso inconveniente para os nossos objetivos, enquanto a complexidade efectiva ε(x) é mais adequada.
No caso da entropia de Shannon, há uma versão relativa semelhante que mede a discrepância informacional entre dois modelos estatísticos, a saber, a divergência de Kullback-Leibler
(5)
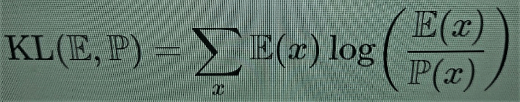
Em termos bayesianos, ela mede a informação obtida ao passarmos da probabilidade prévia P para a posterior E. A complexidade relativa de Kolmogorov (2) pode ser usada, de modo semelhante, como uma forma de distância da informação [4]. É possível construir, usando a complexidade relativa de Kolmogorov, uma noção parecida de complexidade efetiva relativa, ε (x∣y), que também pode ser vista como uma medição de perda/ganho na complexidade informacional.
Então, digamos que algo como ε (x∣y) fornece uma medição possível que leva em consideração se a complexidade informacional é aumentada ou diminuída por um processo que transforma um estado y anteriormente ocupado pelo sistema em um novo estado dado por x. Então, em que ficamos agora? Ainda precisamos de ver como é que isso se relaciona com as redes e a sua estrutura de pequena e grande escala.
Uma ideia da neurociência
Os anarquistas são tradicionalmente avessos à noção comunista de colectividade, contrastando-a geralmente com variados graus de individualismo. A palavra “colectivismo” lembra (com razão) as colectivizações forçadas do estalinismo e a supressão da acção individual. Por outro lado, a palavra “individualismo” constitui facilmente um espantalho para os comunistas, evocando algo como uma combinação linear convexa entre J.D. Salinger e Ayn Rand, concorrendo com os tubarões neoliberais no que se refere ao medo e à supressão da acção colectiva. Essa não é, de modo nenhum, uma situação desejável. A pergunta verdadeiramente importante que devemos fazer é que tipo de “colectividade” maximiza por toda a parte a acção individual, ao mesmo tempo que torna as estruturas colectivas possíveis e interessantes (no sentido da complexidade informacional mencionada anteriormente). Analisarei essa questão à luz de ideias recentemente desenvolvidas no contexto da neurociência, da modelagem de redes cerebrais e da teoria da consciência.
Um esforço considerável de compreensão da estrutura de redes complexas veio da neurociência. Uma ideia que parece especialmente relevante para o que estamos a tentar modelar aqui é a noção de informação integrada, que foi originalmente proposta em [33] como um modelo quantitativo de consciência. Um panorama geral dessa ideia é apresentado em [20], [25].
A ideia central é que a informação integrada mede a quantidade de complexidade informacional num sistema que não pode ser separadamente reduzido às suas partes individuais. É um modo de explicar quão ricas são as possibilidades de inter-relação causal entre diferentes partes do sistema.
Um modo de expressar essa ideia com mais precisão foi desenvolvido em [30]. Consideram-se todas as formas possíveis de dividir um determinado sistema em subsistemas (uma rede em sub-redes locais, por exemplo). Para cada partição λ, considera-se o estado do sistema num determinado momento t, conforme descrito por um conjunto de observáveis Xt, e o estado num tempo futuro próximo Xt+1.
A partição λ em N subsistemas corresponde a uma divisão dessas variáveis Xt={Xt,1,…,Xt,N} Xt+1={Xt+1,1,…,Xt,N} e Xt+1={Xt+1,1,…,Xt+1,N}, em variáveis que descrevem os subsistemas. Todas as relações causais entre os Xt,i, ou entre os Xt+1,j bem como a influência causal dos Xt,i sobre os Xt+1,jao longo da evolução temporal do sistema, são obtidas (estatisticamente) pela distribuição de probabilidade conjunta P(Xt+1,Xt). Para obter a informação integrada do sistema, compara-se o conteúdo da informação dessa distribuição conjunta com o das distribuições em que as únicas dependências causais entre Xt+1 e Xt ocorrem ao longo da evolução em cada subsistema separado, mas não entre subsistemas, o que significa distribuições de probabilidade Q(Xt+1,Xt), com a propriedade de que Q(Xt+1,i∣Xt)= Q(Xt+1,i∣Xt,i), para cada subconjunto i=1,…,Ni=1,…,N da partição. Vamos chamar Mλ o conjunto de distribuições de probabilidade Q(Xt+1,Xt) com essa propriedade em relação à partição λ. Então obtém-se a informação integrada ϕ do sistema ao minimizar-se a divergência Kullback-Leibler (5) entre: a) o sistema atual; e b) sua melhor aproximação por probabilidades que implementam a desconexão causal entre os subsistemas e a avaliação na partição de informação mínima (isto é, minimização sobre a escolha de partição).
(6)
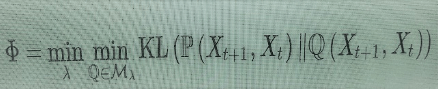
O valor ϕ obtido dessa maneira representa a informação adicional em todo o sistema que não é, de modo algum, redutível às partes menores. É a forma de expressar o conceito de “holístico” em termos informacionais.
Já que estamos mais interessados na complexidade efectiva do que em medidas informacionais, como a divergência de Kullback-Leibler, é possível desenvolver uma versão da informação integrada em que a discrepância entre o sistema e a sua desconexão causal nos subsistemas é medida por uma complexidade efectiva relativa (tal como foi discutido acima) e não pela divergência de Kullback-Leibler (pormenores noutro lugar: esta não é a ocasião para provar novos teoremas).
Pormenores à parte, o que procuramos aqui é fornecer uma medida viável para um processo de optimização. Maximizar a informação integrada (numa versão de complexidade efectiva) significaria obter um sistema que realize a máxima integração possível da complexidade informacional em todos os subsistemas possíveis e o mais alto grau de interconectividade causal dos subsistemas.
É possível perceber por que é que isso faz exatamente o que estamos à procura. Maximizar a informação integrada ϕ favorece a cooperação em lugar da concorrência, uma vez que a concorrência tende a dividir um sistema em competidores separados e isso diminui a função ϕ, enquanto a cooperação aumenta a conectividade e amplia a rede de influências causais mútuas, aumentando ϕ. Além disso, um mecanismo capaz de maximizar ϕ eliminaria fenómenos abomináveis como a propriedade intelectual, já que manter o conhecimento inacessível diminui a sua conectividade causal, reduzindo o valor geral de ϕ. Aumentar ϕ é, em vez disso, compatível com o compartilhamento do conhecimento, redes interpares [Ingl. P2P ou peer-to-peer], etc. Aumentar ϕ não leva à acumulação capitalista de riqueza, uma vez que a concentração de riqueza e recursos tende a separar certos subsistemas e a diminuir a sua influência causal mútua com os demais subsistemas de rede, e isso reduziria a integração geral da complexidade informacional em todo o sistema. A informação integrada é, por definição, uma “colectividade” porque é exactamente a quantidade de complexidade informacional que reside no colectivo sem estar localizada em nenhum subsistema individual separadamente. Por outro lado, é uma colectividade que maximiza a acção individual porque maximiza o grau de influência causal e, portanto, de possível acção, de cada subsistema.
Instrumentos e mecanismos
A dinâmica do lucro nos mercados não é uma lei da natureza: ela é artificialmente implementada através de um dispositivo que contém instrumentos diversos como moedas, sistema de crédito e débito, etc. De maneira similar, se quisermos implementar uma dinâmica de optimização da complexidade informacional integrada, precisaremos de inventar instrumentos apropriados. Essa é uma parcela significativa do problema, claro, mas podemos identificar claramente algumas orientações gerais no interior da noção de uma informação integrada baseada na complexidade efectiva, tal como foi esboçada acima.
Dois aspectos principais podem contribuir para o aumento da grandeza de ϕ: o crescimento da rede de inter-relação causal e o ganho em complexidade efectiva relativa. Assim, podemos identificar, no geral, duas classes de instrumentos que serão úteis para a implementação dessa dinâmica, incrementando, respectivamente, esses dois aspectos da complexidade informacional integrada: chamá-los-ei instrumentos de conectividade e instrumentos de complexidade.
(1) Instrumentos de conectividade
São mecanismos que incrementam o grau de conectividade e a influência causal mútua entre diferentes áreas de uma rede. Podemos incluir entre eles todas as tecnologias que incrementam a conectividade: desde o transporte público (sim, a ferrovia anarquista), redes interpares, redes em malha sem fios em comunidades locais, aplicações distribuídas e escaláveis como Holochain, bibliotecas (tanto físicas quanto virtuais), iniciativas de código aberto e de acesso livre, até objectivos de larga escala como a abolição das fronteiras. O projeto Sci-Hub, desenvolvido pela engenheira informática anarquista Alexandra Elbakyan, do Cazaquistão, é um grande exemplo de um instrumento de conectividade que facilita a livre circulação da ciência.
(2) Instrumentos de complexidade
A cultura gera complexidade efectiva: filosofia, ciência, artes plásticas, música e, sim, poesia! Livros (físicos e digitais), obras de arte, espectáculos: são instrumentos que incrementam a complexidade efectiva. E assim voltamos à visão de Bifo, da poesia contra as finanças [5] [6], que não está propriamente errada: a poesia é um bom exemplo de algo que agrega complexidade, mas não dá lucro. Instrumentos de complexidade são aquelas coisas que costumam ser descartadas na dinâmica dos mercados, em busca do lucro, e são, por outro lado, cruciais para a dinâmica do comunismo cibernético, determinada pela complexidade informacional integrada. Esta é, na verdade, apenas uma visão panorâmica sobre o tipo de instrumentos que sustentarão o dispositivo computacional do comunismo cibernético, em oposição ao dispositivo dos mercados.
Poderíamos (e deveríamos) formular essa ideia de maneira mais precisa. Contudo, já podemos observar, nessa versão simplificada, como a complexidade efectiva e a informação integrada que lhe está associada podem funcionar como uma “valoração objectiva” tal como definida por Kantorovich em [18], em oposição à valoração subjetiva dos preços no mercado.
Para um exemplo de como isso funciona na prática, considere um dos “instrumentos de complexidade” mencionados acima: as artes visuais. Considere as pinturas: num sistema de mercado, o valor da arte está sujeito aos arbítrios do mercado de arte, cujos efeitos completamente devastadores sobre a arte contemporânea, a partir dos anos 1980, foram discutidos com profundidade em [17]. Num sistema comunista cibernético, a arte é um instrumento para o incremento da complexidade. A sua valoração objetiva é a essência da complexidade efectiva. É claro que essa avaliação pode ser feita em vários níveis, começando pela relação da obra de arte com a sociedade contemporânea. Contudo, para simplificar, focar-nos-emos apenas naquilo que pode ser considerado a sua dimensão “estética”. Esse é geralmente o aspecto mais difícil de avaliar, o mais subjectivo, porém, estamos só a tentar estimar a sua eficácia enquanto gerador de complexidade. Se examinarmos o modo como as pinturas de diferentes movimentos artísticos ao longo da história da arte se distribuem num plano com coordenadas baseadas na entropia de Shannon e na complexidade de Kolmogorov (como fiz em [32]), descobriremos uma distribuição interessante, onde movimentos artísticos como o Minimalismo, a Pintura de Campo de Cor [color field painting] e a Arte Conceptual têm valores mais altos de complexidade e valores mais baixos de entropia; outros como a Abstracção Lírica, o Expressionismo Abstracto e a Arte Óptica [Op Art] têm valores intermediários de ambos, e outros como o Cubismo, o Tachismo ou Pontilhismo têm valores altos de entropia e baixos de complexidade.
Mais interessante, porém, é que, em termos de função de informação total (que, como foi anteriormente relembrado, é a soma da entropia de Shannon com a complexidade de Kolmogorov e é a base para a definição da complexidade efectiva), todos esses movimentos artísticos possuem valores muito similares, visto que (como foi demonstrado em [32]), no plano entropia-complexidade (H,K), eles distribuem-se em torno de uma linha de soma constante K+H. Isso corrobora a ideia de que as artes visuais (a pintura, neste caso) funcionam como instrumentos de complexidade com uma certa capacidade objectiva para a geração de complexidade efectiva. Essa concepção das artes e da cultura e do seu papel crucial na dinâmica do desenvolvimento socialista aproxima-se bastante da poderosa concepção original da vanguarda anarco-comunista nas vésperas da Revolução Russa e nos anos seguintes, antes de o estalinismo a ter destruído completamente [1], [8], [15].
Redes multiestratificadas
No modelo proposto para o problema da escala, a passagem do pequeno para o grande ocorre através da conectividade. Estamos a supor que uma organização anarco-comunista funciona bem em pequena escala, o que significa que dispomos de cooperativas de trabalhadores e outras iniciativas similares geridas em conformidade com princípios anarco-comunistas. O processo de maximização, conectando-as, baseia-se em estruturas em rede. Podemos supor que os nós de uma rede são cooperativas, já que não precisamos encontrar uma solução mais sofisticada para a pequena escala. Mas pensar apenas numa rede de conexões é inadequado: o que precisamos realmente são múltiplas redes interconectadas, que representem diferentes modalidades de compartilhamento (ou diferentes modalidades de serviços, de recursos, de informações). O modelo apropriado para esse tipo de estrutura é fornecido pela teoria das redes multiestratificadas [7]. Ele permite expressar não apenas a existência simultânea de diferentes estruturas de rede representando diferentes modalidades de compartilhamento, como também o modo como cada camada se modifica ao longo do tempo de maneira dinâmica, na interação com as outras camadas.
De maneira geral, é preciso compreender que cada um desses “instrumentos” gera a sua própria camada numa rede multiestratificada, com interdependências entre todas as outras camadas. Em geral, quando estudamos grandes redes complexas, sujeitas a mudanças contínuas o tempo todo, é melhor trabalhar com uma abordagem probabilística, considerando as estruturas em rede como um conjunto de mecânica estatística, em que certas propriedades gerais estão fixadas como constrangimentos, e considerando as probabilidades de conexão entre os nós, seja no interior (infracamada) ou através (intracamada) das camadas. São vários os modelos possíveis para o crescimento de uma rede: em particular, em redes de colaboração, parecidas com os modelos que estamos a considerar, costumam ser utilizados fechamentos triádicos. Isso significa que, quando um novo nó é conectado a um nó mais antigo, outros nós que já colaboram com o mais antigo (nós vizinhos na rede) têm maior probabilidade de também se conectarem ao novo nó. Além disso, podemos levar em consideração algumas funções de perda: por exemplo, para camadas da rede que projectam a distribuição física de serviços, a distância geográfica é uma perda, embora ela seja irrelevante para o compartilhamento de informações (havendo uma infraestrutura de rede, como a Internet, já incorporada por outra camada). Esse é outro exemplo de como as valorações que projetam a minimização de perdas, no sentido da programação linear, são dependentes da camada da rede e da escala.
No que diz respeito à parte mais interessante do processo de optimização, a maximização da complexidade informacional integrada, podemos considerar uma dinâmica de rede que generalize modelos convencionais de maximização da entropia de Shannon [7].

Comunidades
As comunidades desempenham um papel importante para desenvolver uma dinâmica baseada na optimização da complexidade informacional integrada numa rede multiestratificada. Elas são estruturas intermediárias entre os nós individuais e a rede de larga escala como um todo.
As comunidades são uma noção familiar no anarquismo: elas são às vezes concebidas em termos de identidade, especialmente em contextos como descolonização, culturas indígenas e organizações de defesa de grupos oprimidos. Elas também se podem formar em torno de projectos compartilhados e iniciativas específicas. Tudo isso é de vital importância para o projeto anarquista. Como a interseccionalidade nos tem ensinado, no que se refere à compreensão das formas de opressão, as noções de identidade e comunidade são ténues e a sua estrutura sobreposta é significativa. No caso das redes complexas, geralmente há muitas comunidades sobrepostas, algumas facilmente detectáveis na estrutura de conectividade da rede, outras mais difíceis de identificar, mas importantes para a determinação das propriedades de escala da rede.
A estrutura das comunidades (as propriedades de modularidade da rede) pode ser considerada um degrau intermediário entre a pequena escala dos nós individuais e sua conectividade local e as estruturas de larga escala. Existem vários métodos algorítmicos para a identificação de comunidades em redes [7]. No caso das redes multiestratificadas, queremos também compreender o modo como comunidades de uma camada se relacionam com comunidades de outras camadas (se a estrutura das comunidades permanece similar ou se sofre modificações significativas através das camadas) e também que partes de diferentes camadas devem ser consideradas parte das mesmas comunidades.
Complexidade informacional e comunidades de rede
Uma medida informacional de proximidade na estrutura de comunidade de diferentes camadas de redes multiestratificadas é fornecida pela informação mútua normalizada. Dada uma estrutura de comunidade com comunidades σ na camada Lα e comunidades σ’ na camada Lβ, a informação mútua normalizada é dada por
(7)
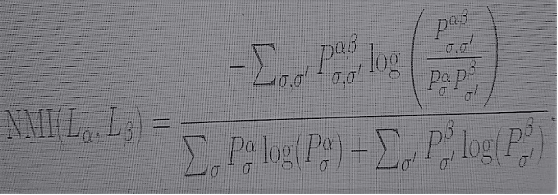
onde
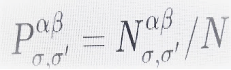
é a fracção de nós que pertencem simultaneamente às comunidades σ na camada Lα e σ’ na camada Lβ,
e, similarmente, ![]() e
e ![]()
são as fracções de nós da comunidade σ na camada Lα, e da comunidade σ’ na camada Lβ, respectivamente. O numerador de (7) é uma divergência de Kullback-Leibler, como em (5), que mede a diferença entre a estrutura de comunidade das duas camadas juntas e a obtida se as duas camadas fossem completamente independentes, enquanto o denominador a normaliza, no que diz respeito à entropia total de Shannon das estruturas de comunidade das duas camadas, consideradas como independentes.
Aqui a comparação, através da divergência de Kullback-Leibler, da distribuição conjunta de nós nas comunidades entre os dois estratos, dada por 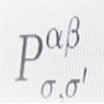
com o de estratos independentes, dados pelo produto ![]() , é claramente uma reminiscência de informação integrada (6) e pode, de facto, ser transformada em uma medida de informação integrada, considerando todas as estruturas de comunidade possíveis nas camadas da rede, assim como se considera todas as partições possíveis de um sistema em (6). Podemos, então, dar o passo seguinte e substituir a entropia pela complexidade efetiva e ponderar as estruturas de comunidade através das camadas em termos de uma complexidade efetiva relativa normalizada. Isso fornecerá um modo de definir uma dinâmica de redes complexas que implementa, de pequenas a grandes escalas, a optimização da complexidade informacional integrada, como uma alternativa à optimização do lucro dos modelos de mercado.
, é claramente uma reminiscência de informação integrada (6) e pode, de facto, ser transformada em uma medida de informação integrada, considerando todas as estruturas de comunidade possíveis nas camadas da rede, assim como se considera todas as partições possíveis de um sistema em (6). Podemos, então, dar o passo seguinte e substituir a entropia pela complexidade efetiva e ponderar as estruturas de comunidade através das camadas em termos de uma complexidade efetiva relativa normalizada. Isso fornecerá um modo de definir uma dinâmica de redes complexas que implementa, de pequenas a grandes escalas, a optimização da complexidade informacional integrada, como uma alternativa à optimização do lucro dos modelos de mercado.
Conclusão provisória
Os mercados são frequentemente propostos, ainda que numa perspectiva anarquista, como um modelo computacional para a abordagem do problema da escala. Podem ser concebidos modelos computacionais alternativos, que não se baseiam no lucro, mas na optimização de uma forma de complexidade informacional integrada. Isso pode proporcionar uma alternativa ao sistema de mercado, para o enfrentamento do problema da escala numa perspectiva anarco-comunista. O objectivo deste ensaio foi o de esboçar algumas dessas ideias, evitando grande parte dos tecnicismos envolvidos. Ele não deve ser considerado de forma alguma uma abordagem definitiva, pois o problema discutido aqui está bastante inexplorado e necessitaria de uma elaboração teórica bem mais extensa.
Junho de 2020
……………………………………………………………………………
[*] Interpolar é empregado aqui na sua acepção matemática. Em matemática, denomina-se interpolação o método que permite construir um novo conjunto de dados a partir de um conjunto discreto de dados pontuais previamente conhecidos.
……………………………………………………………………………….
N.B. A imagem de destaque e as fotos no texto de Aurora Apolito, assim como as suas legendas, foram acrescentadas por mim, José Catarino Soares, o responsável por este blogue. Se necessário for, assumirei a responsabilidade pela sua escolha e por quaisquer eventuais deficiências que possam conter. A tradução do texto é minha (ver o original inglês neste mesmo blogue). Antes desta tradução, a revista electrónica brasileira Passa Palavra já tinha publicado uma outra tradução portuguesa do texto original em Inglês.
…………………………………………………………………………………
Referências
[1] Allan Antliff, Anarchist Modernism, University of Chicago Press, 2007.
[2] Nihat Ay, Markus Mueller, Arleta Szkola, Effective complexity and its relation to logical depth, IEEE Trans. Inf. Th., Vol. 56/9 (2010) 4593–4607. [arXiv:0810.5663]
[3] Charles H. Bennett, Logical Depth and Physical Complexity, in “The Universal Turing Machine – a Half-Century Survey” (Ed. Rolf Herken), Oxford University Press, 1988.
[4] Charles H. Bennett, Peter Gács, Ming Li, Paul M.B. Vitányi, Wojciech H. Zurek, Information distance, IEEE Transactions on Information Theory, 44(1998) N.4, 1407–1423.
[5] Franco ‘Bifo’ Berardi, The Uprising: On Poetry and Finance, Semiotext(e), 2012.
[6] Franco ‘Bifo’ Berardi, Breathing: Chaos and Poetry, Semiotext(e), 2019.
[7] Ginestra Bianconi, Multilayer Networks, Oxford University Press, 2018.
[8] John E. Bowlt and Olga Matich, eds., Laboratory of Dreams: The Russian Avant-garde and Cultural Experiment, Stanford University Press, 1996.
[9] William Davies (Ed.), Economic Science Fictions, Goldsmiths Press, 2019.
[10] Jean-Paul Delahaye, Complexité aléatoire et complexité organisée, Editions Quae, 2009.
[11] Murray Gell-Mann, What is Complexity? Complexity, Vol.1 (1995) N.1 [9 pages].
[12] Murray Gell-Mann, Seth Lloyd, Information Measures, Effective Complexity, and Total Information, Complexity, Vol. 2 (1996) 44–52.
[13] Slava Gerovitch, From Newspeak to Cyberspeak. A History of Soviet Cybernetics, MIT Press, 2002.
[14] George Gorelik, Bogdanov’s Tektology, General Systems Theory, and Cybernetics, Hemisphere Publishing, 1987.
[15] Nina Gourianova, The Aesthetics of Anarchy: Art and Ideology in the Early Russian Avant-Garde, University of California Press, 2012.
[16] Simon Ings, Stalin and the Scientists: A History of Triumph and Tragedy, 1905–1953, Open Road & Grove Atlantic, 2017.
[17] Annamma Joy, John F. Sherry, Jr., Disentangling the paradoxical alliances between art market and art world, Consumption, Markets & Culture, Vol.6 (2003), N.3, 155–181.
[18] Leonid Vitaliyevich Kantorovich, Mathematical methods of organization and planning of production, Leningrad State University Press, 1939.
[19] Anatoly Kitov, Aleksei Lyapunov, Sergei Sobolev, The Main Features of Cybernetics, Voprosy filosofii (Problems of Philosophy), No. 4 (1955), 136–148.
[20] Christoph Koch, The feeling of life itself, MIT Press, 2019.
[21] Nikolai Krementsov, A Martian Stranded on Earth: Alexander Bogdanov, Blood Transfusions, and Proletarian Science, The University of Chicago Press, 2011.
[22] David A. Lax, Libermanism and the Kosygin reform, University of Virginia Press, 1991.
[23] Ming Li, Paul Vitányi, An Introduction to Kolmogorov Complexity and Its Applications, Springer, 1997 [New Edition, 2008].
[24] Evsei G. Liberman, Plans, Profits, and Bonuses, Pravda, September 9, 1962.
[25] Marcello Massimini, Giulio Tononi, Sizing up consciousness, Oxford University Press, 2018.
[26] Warren S. McCulloch, A Heterarchy of Values Determines by the Topology of Nervous Nets, Bulletin of Mathematical Biophysics, 7 (1945) 89–93.
[27] Eden Medina, Cybernetic Revolutionaries. Technology and Politics in Allende’s Chile, MIT Press, 2011.
[28] Benjamin Peters, How Not to Network a Nation. The Uneasy History of the Soviet Internet, MIT Press, 2016.
[29] Ethan Pollock, Stalin and the Soviet Science Wars, Princeton University Press, 2006.
[30] M. Oizumi, N. Tsuchiya, S. Amari, Unified framework for information integration based on information geometry, PNAS, Vol. 113 (2016) N. 51, 14817–14822.
[31] Jaeweon Shin, Michael Holton Price, David H. Wolpert, Hajime Shimao, Brendan Tracey, Timothy A. Kohler, Scale and information-processing thresholds in Holocene social evolution, Nature Communications (2020) 11:2394 https://doi.org/10.1038/s41467-020-16035-9
[32] Higor Y. D. Sigaki, Matjaž Perc, Haroldo V. Ribeiro, History of art paintings through the lens of entropy and complexity, PNAS, Vol.115 (2018) N.37, E8585–E8594
[33] G. Tononi G (2008) Consciousness as integrated information: A provisional manifesto, Biol. Bull. 215 (2008) N.3, 216–242.
[34] Anatoly Vershik, L.V.Kantorovich and Linear Programming, arXiv:0707.0491.
[35] Norbert Wiener, Cybernetics, or control and communication in the animal and the machine, MIT Press, 1948.
……………………………………………………………………………..
 [*] Aurora Apolito é uma matemática e física teórica. Investiga também em linguística e neurociência. Estudou física na Itália e matemática nos EUA, e trabalhou até à data para várias instituições científicas nos EUA, no Canadá e na Alemanha. Aurora Apolito é um pseudónimo literário inventado para diferenciar a sua investigação em filosofia política do seu trabalho noutros campos.
[*] Aurora Apolito é uma matemática e física teórica. Investiga também em linguística e neurociência. Estudou física na Itália e matemática nos EUA, e trabalhou até à data para várias instituições científicas nos EUA, no Canadá e na Alemanha. Aurora Apolito é um pseudónimo literário inventado para diferenciar a sua investigação em filosofia política do seu trabalho noutros campos.