Anarchism and the scale problem

The problem of scale is perhaps the most fundamental problem of anarchism.

We all know by direct experience that anarchism works well on a local scale. Most people who have been active in the anarchist movement have also participated in at least some initiatives such as Food-Not-Bombs, infoshops, small publishing houses, anarchist bookfairs, mutual aid initiatives, Antifa, worker-owned cooperatives, street medics, hacker and maker spaces, etc. The anarchist movement has a huge accumulated historical experience on how to run such local community initiatives. There is little doubt that anarchism works on what I will refer to as “the small scale”.

Historically, one of the main forms of criticism levelled against anarchism has been that it does not provide a convincing theory of how a decentralized, non-hierarchical form of organization can be scaled up to work efficiently on “the large scale”. This objection has often been voiced by socialist and communist militants who advocate forms of planning centered around a party structure and/or a state organization. Famously, Leon Trotsky in his autobiography commented on how his early enthusiasm for anarchism cooled when his anarchist comrades were unable to provide a good plan for how to run the railway system. Trotsky’s writing was disingenuous, but the question is legitimate. How does anarchism handle large scale structures? Is there a good scaling strategy that interpolates from the small to the large? Although one can certainly envision several good answers to the specific railway problem, the more general problem of scale is highly nontrivial: it is well known that many physical systems are not scale-free and break down outside of a typical scale of applicability. Is anarchism such a system, destined to only work in the scale of small local communities?

There is a part of the anarchist movement that has retreated on such “local” positions and advocated abandoning the scale problem entirely, focusing only on action and organization at the level of small communities. I maintain that this position is incompatible with the broad ideals of anarchism, whose ultimate goal is the liberation of all humanity (and all sentient entities, biological or mechanical) from oppression and hierarchical power structures. To achieve such goals modern anarchism has to engage with a world of high complexity and multiple layers of large scale structures. Retreating inside the comfort zone of small homogeneous local communities runs contrary to anarchism’s entire history of grand aspiration and visionary revolutionary ideas. There are other, very different, tendencies within the anarchist movement, such as “Left Market Anarchism”, that do not shy away from facing the problem of scale, but in essence advocate solving it by borrowing the market mechanism from capitalism, and somehow “liberating” it to serve more just socio-economic goals and a more equal society. I find this approach also unappealing. I don’t believe that markets can be “liberated” from capitalism, nor that they can do anything good anyway, regardless of their liberated status. In essence, this is because I view the market mechanism as running on a steepest descent towards a cost/energy minimum, in an attempt to maximize profit, which inevitably singles out the least valuable options, while wiping out anything that is of any value (but is not profit-making) along the process. Call it my communist prejudice.

For the purpose of this brief essay, I only want to discuss some aspects of the scale problem under some simplifying assumptions that I feel confident about when I try to envision the structure of an anarchist society (or at least one I would feel comfortable living in). So, I am going to start by assuming that what happens at the “small scales” is established in the form of a network of communes, cooperatives, and collectives, which are run on anarcho-communist forms of organization, and I will consider the question of how to introduce large scale structures over this network.

What I mean here by “large scale structures” can be primarily described as “large scale distribution of services”. Services include all the obvious needs such as transportation (the anarchist railway!), health care, production and distribution of knowledge (connectivity, learning, circulation and accessibility of information), the chain of supply of food and materials. All of these typically cannot be handled strictly within the level of a local community, regardless of how well planned and efficient local food production or local public transportation can be made. Services are not cost-effective, precisely because they are services. The advantage of their existence is enormous, but it manifests itself in indirect ways that do not result in profit in the running of the services themselves. This is why it is impossible to expect good services under capitalism: car-based transportation is inefficient and environmentally disastrous, knowledge is kept hostage behind paywalls, health care is inaccessible, production and supply focus on fast consumption of low quality content, and so on.

On the other hand, a broad and disparate range of political positions within the socialist spectrum, ranging from the social democracies to authoritarian Stalinism, have traditionally invested the state with the task of attending to large scale distribution of services. This conflation of state and services has the dangerous effect of coupling a useful function (providing reliable access to services) to the most unpleasant and authoritarian aspects of the state: a large sector of production is siphoned off in the service of the military, enforcement is delegated to the violent action of the police, inefficiencies abound, and centralization often makes planning unreliable. I will discuss in some detail some attempted alternatives, developed historically within the socialist/communist perspective, that aimed at decentralization and decoupling of services and state power.

Communism and the scale problem

A first observation I’d like to make before discussing the scale problem further is that one can easily turn the table on the “scaling objection”, that has been historically addressed as a problem of anarchism, and formulate the same scaling question as a problem of communism. Assuming that at the local scale a communist economic system is implemented efficiently in terms of workers owned cooperatives and communes, how does it scale to involve the entire chain of supply and the large scale services? Historically, communism has usually resorted to centralized planned economies, often resulting in disastrous mismanagements, paired with oppressive authoritarianism. However, there are several useful and interesting lessons to extract from the many unsuccessful attempts that were made historically at decentralizing the communist economic planning and the difficulties that those attempts encountered.

During Soviet times, there were two main significant attempts to bring computational methods to bear on the problem of scale in the planned economy. One was Leonid Kantorovich’s linear programming [18], which, after an initial phase of strong obstruction and suppression from the authorities during Stalin’s time, started to be recognized around the end of the 1950s, [34]. Linear programming techniques were later adopted in Soviet economic planning, starting with the military production chain in the 1960s.

While Kantorovich’s optimization methods were explicitly designed for an efficient allocation of resources in a communist economy, the extreme opposition they encountered in Stalinist times was largely due to the perceived similarities between Kantorovich’s “valuations” and a market pricing system. While this is not the main topic I want to focus on in this essay, I would like to stress the fact that being against borrowing market mechanisms from capitalism does not (and should not) imply a blank rejection of the use of mathematical optimization methods as part of a communist economy.

Even in a post-scarcity scenario, with abundant availability of renewable energy, certain materials would remain scarce, simply due to the different relative distribution of the chemical elements in the universe. Avoiding wastefulness and minimizing environmental impact would remain valuable goals. Such minimization problems are indeed well handled by techniques such a linear programming and are easily agreed upon. It is maximization goals that present the hard part of the question in our scaling problem.

The issue is not whether forms of optimization are in themselves helpful, but rather what is being optimized. The main problem, which I will return to, is that when it comes to the distribution of services in a large-scale form of communist economy, a much higher level of informational complexity is required to design a valid system of valuations and constraints, one that does not reflect the simplistic capitalist notion of profit, but that can capture advantages that only take place on a much larger spatiotemporal scale and at much deeper complexity levels. Kantorovich’s linear programming approach will also suffer in principle from a scale problem, as valuations are not scale-independent, and the scale-dependence of the complexity required to identify a good system of valuations and constraints is a crucial part of the problem. The markets reliance on profit optimization bypasses the problem, at the cost of killing the solution.

The other historical attempt to introduce computational methods to address the scale problem in a communist economy, which is generally lesser known but more interesting for the purpose of our discussion, was Victor Glushkov’s cybernetic project of a decentralized network of feedback and computational mechanisms, based on a rudimentary form of artificial intelligence. In this plan, this completely decentralized, vast computational network would have eventually entirely removed the state from the tasks of economic planning and distribution of services. Needless to say, the project was vehemently opposed by the Soviet government, after an initial phase of mild enthusiasm quickly evaporated. A detailed account of the history of this project is presented in [28], while more general background on the role of cybernetics in the Soviet Union is discussed in depth in [13].

History of Cybernetic Communism

During the early days of the Russian Revolution, a significant precursor of cybernetics was proposed in the “Tektology” philosophy of the transhumanist Bolshevik leader Aleksandr Bogdanov, [14], [21].

However, when Norbert Wiener introduced the new science of cybernetics in 1948, [35], it was attacked and condemned by Stalin’s regime, much like several other fields of contemporary science, with the exclusion of what became immediately necessary for the development of nuclear weapons, [16], [29].

Despite the official prohibition, an interest in cybernetics began to grow among Soviet scientists, largely thanks to the private home seminars of the mathematician Aleksei Lyapunov, [13]. The official rehabilitation of cybernetics started only after 1953, the year of Stalin’s death, with a famous paper of Anatoly Kitov, Aleksei Lyapunov and Sergei Sobolev (all heavy weights of the Soviet scientific establishment), [19]. By 1967, cybernetics in the Soviet Union counted five hundred active research institutes and tens of thousands of researchers, [13], [28].

Economic reform became a pressing need in the mid’50s, after Stalin’s rule had left the country in shambles, the chain of supply and the agricultural sector nearing collapse and a serious risk of another major famine looming. Amidst a very rapid expansion of the techno-scientific sector, from the early successes of the Soviet space program to the first large developments of computer systems and automation, several competing proposals for economic reforms were presented that promoted the idea of a “computational solution” to the severe mismanagements of the planned economy.

It was in this setting that the mathematician Victor Glushkov devised a grand plan to wrestle away the communist economy from the centralized planning of the Soviet government and replace its role entirely by a decentralized autonomous computational network. This massive OGAS (All States Automated System) project was presented directly to Khrushchev in 1962, and authorized in an initial phase in 1963. The original design of this decentralized remote computing system was workers-oriented, anti-bureaucratic, and non-hierarchical, [28]. In this cybernetic vision, McCulloch’s concept of heterarchy [26] made it possible to develop an understanding of complex systems outside of the restrictive logic of a dichotomy between hierarchies and at markets, and emphasize instead self-organization, feedback loops, and complex networks, [28].

The original plan of the cybernetics approach was to implement a decentralized computational system, capable of processing feedbacks in real time and handle the simulation of complex dynamics. In terms of providing a scalable computational model, they mostly focused on Kantorovich’s linear programming, which seemed the most promising mathematical tool at the time. As we mentioned, the scalability of Kantorovich’s valuations is subtle, and we will discuss a possible more modern approach to scalability in the next section of this paper. However, the most important aspect of this proposal was the main idea of a cybernetic computational network and its role at implementing a decentralized autonomous computational mechanism for a communist economic system that would not require any centralized planning.

It became rapidly clear that the projected costs of an implementation of this project on the entire territory of the Soviet Union were enormous, but it became even more obvious that the goal of replacing the centralized planning and control of the Soviet government with a decentralized non-hierarchical autonomous computational system were an immediate threat to the establishment.

At around the time of the transition between the Khrushchev and the Brezhnev leadership (1964,1965), the Soviet government opted instead for the much less threatening proposals of the Kosygin-Liberman economic reforms. These were based on Evsei Liberman’s economic plan [22], [24], focused on introducing profit measures and a market mechanism. Thus, the easier and less threatening pro t-driven dynamics of markets effectively killed the much more interesting and possibly revolutionary cybernetic plan for a large decentralized autonomous system that was not based on the profit mechanism. The Kosygin-Liberman reform itself was then eventually abandoned in 1970, [28].

Cybernetic communism did not recover in the Soviet Union, though cybernetics itself continued to enjoy widespread popularity in Soviet culture in the ’70s. However, another experiment in cybernetic communism developed independently in Allende’s Chile. It was nearing completion in the early 1970s, but remained unfinished when the Allende government was violently overthrown by the fascist Pinochet coup [27].

Unlike the Soviet government, that quickly pulled the break on the OGAS project as soon as it perceived it as a threat to its authoritarian control, Allende was genuinely open to the idea of a decentralized non-authoritarian communism, so he enthusiastically embraced the idea of a cybernetic solution. In 1971, the Allende government contacted the socialist British cyberneticist Stafford Beer asking for a consultation on how to implement a distributed decision support system for the management of the national economy that would respect the autonomy of workers and avoid  imposing a top-down chain of control.

Beer enthusiastically accepted the task and became the main architect of the Project Cybersyn, consisting of a broad network of data collecting telex machines, a statistical modeling software, an economic simulator software, and an operation room where human observers could oversee the ow of data and the results of modeling, and respond to possible emergencies. Beer’s main goal was to develop self-regulating factories and assign decision-making power entirely to these workers-owned structures, in a way that would be compatible (through the computational system) with the larger scale national economy. While Cybersyn came much closer to full functionality than its Soviet counterpart, the sudden tragic end of Allende and the descent of Chile into the darkness of fascist dictatorship entirely wiped out the possibility of seeing it to fruition. When the military took over the presidential palace, they destroyed the Cybersyn operations room and entirely dismantled the system, [27].

Communism needs Complexity

Before I move on to describe a more concrete proposal for the problem of scale, I want to argue that scaling a model of organization and production based on anarcho-communist principles is possible only in the presence of enough capacity for informational complexity.

As background I will refer to a recent study [31], where historical data (from the Seshat Global History Databank) of a large range of different polities are analyzed, ranging from village-level societies to empires. The method of Principal Component Analysis (PCA) is applied to the data, which can be mapped to a two-dimensional space given by the first two principal components, capturing most of the variation in the data. When visualized in this way, the data follow a highly structured pattern. Looking at the variation in the second principal component for increasing values of the first one, historical polities show an initial very concentrated phase, which can be interpreted as growth in scale with relatively little growth in information capacity. This is followed by a threshold (which the authors call the “scale threshold”) after which the pattern of polities that grow in scale but hardly in informational complexity starts to diverge significantly from those that achieve a more significant growth in informational capacity. A second threshold (the “information threshold”) makes further growth in scale possible for those polities that have achieved a sufficiently high level of information-processing capacity. There is, correspondingly, a region in this two-dimensional parameterizing space where polities are more spread out, indicating different possible patterns of development in the scale/information landscape. After the second threshold is passed, scale growth becomes prevalent again and polities tend to cluster again in this parameterizing space with less diversified features. The dataset used in this study is tailored to the analysis of pre-modern societies, hence, as the authors point out, the behavior after the information threshold is crossed may look artificially more homogenous, due to the saturation of several of the variables as data of more modern societies are encountered.

Socialism and communism are intrinsically modern phenomena requiring industrial and information societies (primitivists be damned). Nonetheless, one can still derive some useful observations from the analysis carried out in [31]. In particular, while a variety of different forms of organization in small-scale polities occurs, further societal development, when scale grows significantly but constrained by relatively low information-processing capacity, tends to organize in statist authoritarian forms. Wealth inequality typically rises rapidly in this phase. Only after enough informational complexity is reached a variety of different forms of development becomes again possible.

Leaving momentarily aside the question of the reliability of Seshat data for more modern societies, one can interpret the renewed emphasis on scale growth (rather than continued informational complexity growth) after the second phase transition as an aspect of the modern capitalist societies. This would suggest that one should expect another phase transition to a very significant growth in information-managing capacity to be necessary for new non-capitalist forms of organization to become possible at the current level of scale of contemporary societies. In other words, a significant further increase in informational-complexity is necessary for non-authoritarian communism. By contrast, fascism can be seen as an attempt to achieve scale-growth (imperial aspirations) coupled to a dramatic suppression of all levels of complexity.

Historically, societies that attempted to implement a communist system of production, in the absence of a sufficient level of informational-complexity, have relied on centralized planning and fallen back onto authoritarian political forms. Despite this historical experience, many political forces, from the historical Social Democracies, to postwar Eurocommunism (such as the Italian PCI), to current Democratic Socialism, have repeatedly argued that statist solutions to the problem of large scale distribution of services in socialism can exist in non-authoritarian forms. However, such solutions would still be relying on forms of coercion (taxation, police enforcement), to achieve the task of acquisition and distribution of resources. No matter how benign such forms of coercion can be made to appear, in the long term the fact that a working system has to be maintained functional through the threat of force makes it inherently fragile.

Ultimately, both Victor Glushkov’s unrealized cybernetic network in the Soviet Union and Stafford Beer’s unfinished Cybersyn system in Allende’s Chile were attempts to greatly increase the capability of processing informational complexity in their respective societies, as a necessary mean for the possible existence of a decentralized non-authoritarian communism that would scale up to the level of large networks.

Communist objection to Markets

I also want to reiterate here that the main communist objection to markets is that better and more sophisticated mathematics is needed to formulate and address the problem of scale in a communist economy, and in a decentralized non-authoritarian setting, than what is currently offered by borrowing market mechanisms from capitalism. Settling on inadequate mathematical methods will lead to ineffective and undesirable solutions. Capitalism and its disasters can ride the wave of a simple optimization process based on profit, at the cost of widespread devastation, but that is not something one should be trying to emulate. If a problem is both di cult and interesting enough to deserve the de novo development of an appropriate theoretical apparatus, then that is “What needs to be done”, without going along with dubious capitalist shortcuts.

I feel this clarification is needed because there is a widespread tendency to formulate a communist objection to markets in terms of an overall objection to the use of mathematical methods of optimization and analysis. I wish I could just dismiss this as a side effect of the historically dismal state of communism in North America. However, prominent figures in the tradition of European non-authoritarian communism (such as Autonomia) have recently supported this viewpoint, as one can see, for instance, in the recent writings of Bifo, [5], [6]. For instance, one finds in [5] “we can argue that the disentanglement of social life from the ferocious domination of mathematical exactitude is a poetic task, as poetry is language’s excess” and in [6] “Power is today based on abstract relations between numerical entities […] There is no political escape from this trap: only poetry, as the excess of semiotic exchange, can reactivate breathing.”

Despite what Bifo and others suggest, there isn’t any identification be-tween mathematical abstraction and financial capitalism, contrasted with a poetical opposition to abstraction. Stated in these terms, this opposition does not make any sense, not just because poetry is inherently a form of abstraction and mathematics is largely a form of poetical imagination, but because it is precisely our capacity for a poetical mathematical imagination that will make it possible for us to envision a functioning alternative to the world of capitalism and finance. As discussed below in the historical case of Kolmogorov’s linear programming, the blanket opposition to mathematical modeling is purely a Stalinist reaction, not a viewpoint that anarcho-communism should be adopting. Communism is techno-optimist in its very essence: this is something that certain primitivist anti-civ brands of anarchism may find difficult to stomach, but it is inherent in the nature of both socialism and communism that seizing the means of production requires the existence of sufficiently sophisticated means of production worth seizing. Seeking to approach crucial problems such as the distribution of resources and services in a communist economy via a careful scientific and mathematical analysis is the natural approach in a communist setting. Again, if it weren’t for the fact that the current communist (and anarcho-communist) scene has become so weirdly skewed in its views of science and technology, there would be absolutely no need to make such self-evident clarifications.

The profit driven maximization process of markets is not a viable option, not because “profit” is a bad word (it is!) but because of the way the dynamics works: even if one could start with an ideal initial condition of equally distributed wealth, even very small fluctuations will get largely amplified, rapidly reproducing a situation of uneven accumulation. In the profit dynamics of markets an equitable wealth distribution is necessarily an unstable condition. That’s in essence why markets cannot be liberated from capitalism. Markets are an automated generator of capitalist wealth inequalities, which can quickly and easily wipe out any hard-won gains that costed major social upheavals and di cult revolutionary actions to achieve. (We all want a Revolution, but not one that will immediately go wasted just because someone will turn on it the fast-capitalism-restoring-machine commonly known as markets!)

To avoid a runaway reaction of wealth disparity accumulation, one needs to design an entirely different optimization process that does not reside in the market mechanism of profit maximization.

I’ll make a metaphorical comparison to better explain this viewpoint. When, in the history of modern physics, quantum mechanical phenomena were in need of a viable theoretical understanding, physicists did employ methods that had been known and available before, such as linear algebra or linear partial differential equations. This does not mean that directly adapting the mathematical models responsible for the description of classical physics would provide a good model capable of solving quantum mechanical problems. The “hidden variables” debacle showed that a classical physics model of quantum phenomena is actually simply not possible. On the contrary, a completely new mathematical theory, based on Hilbert spaces and operator algebras, was designed entirely for the purpose of describing quantum physics.

When I am saying that one needs to develop the correct mathematical model to be used to solve the scale problem in the anarcho-communist setting, I do not mean that existing methods should not be used as partial building blocks and intermediate steps. As I will discuss in the next section, there is a lot of available theory that will be useful and that should be employed. I am saying that what one should aim for is like what happened with the development of the mathematical theory necessary for a satisfactory predictive description of quantum mechanics: existing models by themselves would not provide a solution and an entirely new theoretical edifice needed to be constructed, even though a few of its basic building blocks were already available in previous theories.

Self-organization in networks and the anarchist scale problem

I am not trying here to present a solution to the scale problem in anarchism, but to highlight what I think are some important aspects that can hopefully lead to a more precise formulation of the problem. This section is going to be more technical, as I will review some methods in the analysis of complex networks, which I believe have to be regarded as part of the necessary tools to approach the scale problem in an anarchist setting.

A fundamental premise, in order to formulate more precisely the problem of scale in anarchism, is that anarchism is at heart a process of self-organization in complex networks. Phenomena of self-organization in networks are widely studied in the theory of complex systems, motivated by a range of models from telecommunication systems to neuroscience. However, what one needs to develop goes beyond a rephrasing or a direct application of these models. What I would like to outline here is a brief overview of what I see as the more crucial and more di cult aspects of the problem.

Ludwig von Mises, in his notorious 1920 essay promoting markets over the then rapidly developing trend toward socialist economic planning, aimed at presenting markets as an efficient computational machinery. As discussed in the introductory essay of [9]. “The challenge that Mises laid down for socialism was a resolutely technocratic one: to come up with a rival infrastructure of computation that could match that of the price system […] It was a challenge that few socialists have been successfully able to duck altogether, and fewer still have successfully risen to”.

The lack of a convincing development of such a “rival socialist infrastructure of computation” is highly regrettable. However, to be honest, it is quite possible that the mathematics required to provide a viable socialist/communist answer to Mises’ challenge had simply not been available at the time, and for quite a long time after that. Even at the time of the main attempts at implementing forms of Cybernetic Communism, in the ’60s and early ’70s, the theory of complex networks was still in its infancy. It is likely that, despite having the correct general idea in mind, the efforts of both Victor Glushkov and Stafford Beer would have failed when implemented within the available science and technology framework of the time, simply because the information processing capacity was still too low and some crucial mathematical tools still unavailable. We are in a much better position today to provide a viable opposition to markets, so there is no excuse any longer for eschewing this task.

What I am writing in this section should be regarded as an exercise in the kind of “Economic Science Fictions” that are discussed at length in [9] and in the kind of mathematical imagination I was mentioning above. It is meant to envision the mathematical form of a cybernetic communist infrastructure of computation that would replace the profit optimization mechanism of markets.

Complexity 

First and foremost, complexity is the key notion here, but it is also a very subtle one, which is not easy to measure. The main notion of complexity in mathematics is Kolmogorov complexity, which classifies the complexity of something as the length of the shortest process (algorithm) that realizes it, [23]. Namely,

(1)

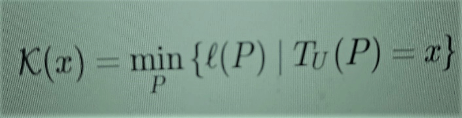
which means that complexity of x is the minimal length l (P) among all programs P with the property that, when run on a universal computer (Turing machine) T_U, will output x. I am writing this out explicitly, because it makes it easier to compare with other notions, and also because I want to mention also the “relative complexity” version, which I will return to later. This is given by

(2)

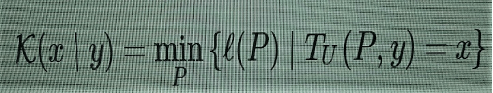
which is the same thing, but the computing machine T_U is allowed to use the input y in addition to the program P to compute x.

Kolmogorov complexity is itself a non-computable function, because of the fact that the “halting problem”, deciding whether a program will run forever or will halt at some point with an output, is itself an undecidable problem. Surprisingly, the non-computability itself is not a serious obstacle, because Kolmogorov complexity has lots of perfectly good computable upper bounds (by any compression algorithm), hence it cannot be computed but it can be approximated by excess in a computable way. There is another more serious drawback to the use of Kolmogorov complexity though: it does not correspond to the intuitive notion of complexity one would like to model, in the sense that, while it correctly assigns low complexity to easily predictable patterns, it is maximal on completely random patterns. Maximizing randomness is clearly not what one would like to achieve, despite what naive misconception of anarchism circulating among liberals would suggest. Shannon entropy is close to an averaged version of Kolmogorov complexity,

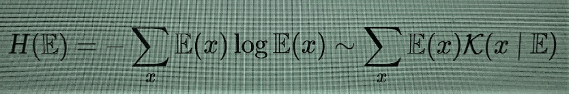
and it has the same tendency to detect randomness, so by itself it also does not help.

There are possible ways to devise measures of complexity that are better targeted at detecting “structured complexity” rather than complexity due to the unpredictability of randomness. A first possible modification of Kolmogorov complexity that better captures some form of “organized complexity” is given by logical depth. This notion was introduced in [3], using the execution time of a nearly-minimal program rather than the length of the minimal program as in the Kolmogorov case. Namely,

(3)

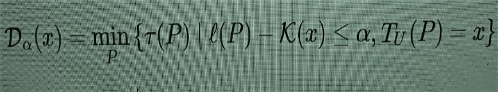
which means computing the minimum time of execution of a program P that outputs x, whose length is equal to or just slightly larger than the minimum one (whose length is K(x)). How much length discrepancy is allowed between the minimal one K(x) and ℓ(P) is measured by a variable parameter. (More precisely, one uses a slightly different form of Kolmogorov complexity K(x) in (3), but I will not go into the details here: they can be found in [2].) Passing from minimal to nearly-minimal is just meant to avoid the problem that some slightly longer programs may have shorter execution time. More interestingly, passing from length of a program to its execution time may seem at first like a minor change, since execution time may be seen as another form of length (in time rather than memory), but the effect is significant on reducing the role of randomness in high complexity patterns. A comparative discussion of Kolmogorov complexity and logical depth can be found in [10]. The reason why I don’t want to use this simple modification of Kolmogorov complexity is because of a “phase transition” phenomenon described in [2] that I will describe in a moment, which makes logical depth di cult to use as the basis for the construction of an optimization function.

Murray Gell-Mann proposed a notion of “effective complexity” and a notion of “potential complexity” [11], which were meant to capture more closely the intuitive notion we have of complexity as a highly structured phenomenon. Effective complexity is meant to capture the information content of the “regularities” of a pattern, while potential complexity is a similar notion that is meant to incorporate changes in time. A first mathematical account of effective complexity was given in [12]. Unfortunately, neither of these notions has yet a completely well developed mathematical formalism. We can, nonetheless, start from where things stand at the moment in terms of these more promising notions of complexity and see what can be done with them. A good overview of the situation with these complexity measures is given in [2], which I will refer to for my brief summary here. In order to obtain a good working description of effective complexity one first considers a combination of Kolmogorov complexity and Shannon entropy, called the “total information” K(E)+H(E). It can be described as the algorithmic complexity of computing x (Kolmogorov part K(x∣E)) through computing the statistical ensemble E that x belongs to (Shannon part H(E)).

The best choice of statistical ensemble E for a given x is selected by the requirement that it minimizes the total information, which is a way of saying that it is the most likely explanation for the datum x. Having selected the appropriate statistical model E, one can detect if the element x is “typical” in that statistical ensemble, by checking that the probability E (x) is not much smaller than an average size 2^−H(E) predicted by the Shannon entropy. Given x, one selects in this way the set M_x of all the possible ensembles E with small total information and for which x is typical (possibly with additional constraints on what set of “good theories” one wants to consider). The “effective complexity” ε(x) is the minimal value of Kolmogorov complexity K(E) among all these candidate models E,

(4)

Note how we are defining effective complexity here as a minimum of Kolmogorov complexity over a certain set of statistical models E explaining the given datum x, as a way of saying that we want to single out the simplest explanation, selected among a set of plausible theories. This seems to contrast the fact that I earlier mentioned, namely that we aim for a maximization of informational complexity. However, that maximization is still to come: the minimization I just describes is simply a necessary preliminary step that assigns an appropriate complexity value to a datum.

What has one gained by using effective complexity ε(x) rather than Kolmogorov complexity K(x) or Shannon entropy H(E)? The main advantage is that now completely random patterns have small effective complexity! So, objects with large effective complexity are caused by “structured complexity” rather than by randomness. It is not immediately obvious that effective complexity of random patterns is small: a proof of this fact is given, for instance, in Theorem 10 of [2], while some cases of non-random patterns that do exhibit large effective complexity are described in Theorem 14 of [2].

The “phase transition” phenomenon I mentioned above for the behavior of logical depth is based on how D_α(x) changes compared to effective complexity ε(x). It can be shown (see Theorem 18 of [2] for details) that for small values of ε(x) logical complexity can also take small values, but when effective complexity crosses a threshold value (which depends on Kolmogorov complexity), the logical depth suddenly jumps to extremely large values. This sudden phase transition in the behavior of D_α(x) makes it inconvenient to use for our goals, while effective complexity ε(x) is more suitable.

In the case of the Shannon entropy, one has a similar relative version that measures the informational discrepancy between two statistical models, namely the Kullback-Leibler divergence

(5)

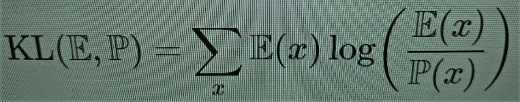
In Bayesian terms it measures the information gained by passing from the prior probability Pto the posterior E. Relative Kolmogorov complexity (2) can be used in a similar way as a form of information distance, [4]. One can construct, using relative Kolmogorov complexity, a related notion of relative effective complexity, ε(x∣y), which can also be seen as a measure of loss/gain in informational complexity.

So, let’s say that something like this ε(x∣y) provides a candidate measurement taking into account whether informational complexity is increased or decreased by a process that changes the state y previously occupied by the system into a new one given by x. Now what? We still need to see how this relates to networks and their small and large scale structure.

An idea from Neuroscience

Anarchists are traditionally wary of the communist notion of collectivity, often contrasting it with varying degrees of individualism. The word “collectivism” rings (justified) alarm bells about Stalinist forced collectivizations and suppression of individual agency. On the other hand, the word “individualism” provides an easy strawman for the communist, conjuring up a mental image of some kind of convex linear combination between J.D. Salinger and Ayn Rand, pandering to neoliberal sharks the fear and suppression of collective agency. This is not overall a productive state of affairs. The actual important question one should ask instead is what is a form of “collectivity” that everywhere locally maximizes individual agency, while making collective emergent structures possible and interesting (in the same informational complexity sense described previously). I will discuss this question in the light of ideas recently developed in the context of neuroscience, the modeling of brain networks, and the theory of consciousness.

A considerable amount of work in understanding the structure of complex networks has come from neuroscience. An idea that seems especially relevant to what we are trying to model here is the notion of integrated information, which was originally proposed in [33] as a quantitative model of consciousness. A general overview of this idea is presented in [20], [25].

The key idea is that integrated information measures the amount of informational complexity in a system that is not separately reducible to its individual parts. It is a way to account for how rich are the possibilities of causal relatedness among different parts of the system.

A way to express this idea more precisely was developed in [30]. One considers all possible ways of splitting a given system into subsystems (a network into smaller local subnetworks for example). For each such partition λ one considers the state of the system at a given time tas described by a set of observables X_t and the state at a near-future time X_t+1.

The partition λ into N subsystems corresponds to a splitting of these variables X_t={X_t,₁,…,X_t,_N} X_t+1={X_t+1,₁,…,X_t,_N} e X_t+1={X_t+1,₁,…,Xt+_1,N}, into variables describing the subsystems. All the causal relations among the X_t, themselves, or among the X_t+1, as well as the causal influence of the X_t,_i  on the X_t+1,_j through the time evolution of the system, are captured (statistically) by the joint probability distribution P(X_t+1,X_t). To capture the integrated information of the system, one compares the information content of this joint distribution with that of distributions where the only causal dependencies between X_t+1 and X_t  is through the evolution within each separate subsystem but  not across subsystems, which means probability distributions Q(X_t+1,X_t),  with the property that Q(X_t+1,_i∣X_t)= Q(X_t+1,_i∣X_t,_i) for each subset i=1,…,N_i=1,…,N  of the partition. Let’s call M_λ the set of probability distributions  Q(X_t+1,X_t) with this property with respect to the partition λ. One then obtains the integrated information of the system by minimizing the Kullback-Leibler divergence (5) between the actual system and its best approximation by probabilities that implement the causal disconnection between the subsystems and evaluating at the minimal information partition (that is, minimizing over the choice of partition).

(6)

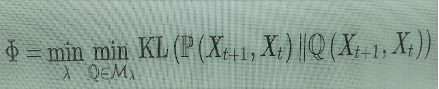
The value obtained in this way represents the additional information in the whole system that is not in any way reducible to smaller parts. It is the way to express the concept of “holistic” in informational terms.

Since we are more interested in effective complexity than in informational measures such as the Kullback-Leibler divergence, one can develop a version of integrated information where the discrepancy between the system and its causal disconnection into subsystems is measured by a relative effective complexity (as discussed above) rather than by the Kullback-Leibler divergence (details elsewhere: this is not the place where to prove new theorems).

Details aside, what we are aiming for here is to provide a viable measure for an optimization process. Maximizing integrated information ϕ (in an effective complexity version) would mean obtaining a system that realizes the maximal possible integration of informational complexity across all possible subsystems and the highest degree of causal interconnectedness of subsystems.

We can see why this essentially does what we have been looking for. Maximizing our integrated information favors cooperation over competition, since competition tends to break apart a system into separate competitors and this decreases the function ϕ, while cooperation increases connectedness and enlarges the network of mutual causal influences, leading to an increase of ϕ. Also a mechanism that maximizes would wipe out abhorrent phenomena like intellectual property, since keeping knowledge inaccessible decreases its causal connectedness, decreasing the overall value of ϕ. Increasing is instead compatible with forms of shared knowledge, P2P networks, etc. Increasing ϕ does not lead to capitalist wealth accumulation, since concentration of wealth and resources tends to separate out certain subsystems and decrease their mutual causal influence with the rest of the network subsystems, and this would decrease the overall integration of informational complexity across the entire system. Integrated information is by definition a “collectivity” because it is exactly the amount of informational complexity that resides in the collective without being located in any separate individual subsystem. On the other hand, it is a collectivity that maximizes individual agency because it maximizes the degree of causal influence, hence of possible agency, of each individual subsystem.

Instruments and Mechanisms

The dynamics of profit in markets is not a law of nature: it is implemented artificially via a machinery consisting of several instruments such as currencies, systems of credit and debt, etc. In a similar way, if we want to implement a dynamics of integrated informational complexity optimization, we need to devise the appropriate instruments that will implement it. This is a significant part of the problem, of course, but some general guidelines are clearly discernible within our notion of a form of integrated information based on effective complexity, as outlined earlier in this section. There are two main aspects that can contribute to increasing our measure ϕ: the growth of the network of causal relatedness and the gain in relative effective complexity. Thus, we can identify, broadly, two classes of instruments that are useful in implementing this dynamics by respectively increasing these two aspects of integrated informational complexity: I will call them instruments of connectedness and instruments of complexity.

• Instruments of connectedness. These are mechanisms that will increase the degree of connectedness and mutual causal influence between all different areas of a network. We can include among them all technologies that increase connectedness: public transportation (yes, the anarchist railway), P2P networks, wireless mesh networks for local communities, scalable distributed computing resources like Holochain, libraries (both physical and virtual), open source and open access initiatives, all the way to grander scale goals such as border abolition. The Sci-Hub project developed by the Kazakhstani anarchist computer scientist Alexandra Elbakyan is a great example of an instrument of connectedness facilitating the free circulation of science.
• Instruments of complexity. Culture generates effective complexity: philosophy, science, the visual arts, music, and yes, poetry! Books (physical and digital), art works, performance: these are all instruments that increase e effective complexity. Coming back to Bifo’s image of poetry against finance, [5], [6], in the appropriate sense he was not wrong: poetry is a good example of something that grows complexity but not profit. Instruments of complexity are typically what would be wiped out by the profit-driven dynamics of markets, and are instead crucial to the cybernetic communism dynamics driven by integrated informational complexity.

This is of course only a quick bird-eye view of the kind of instruments that feed the computational machinery of cybernetic communism, in opposition to the machinery of markets. Things could (and should) be formulated more precisely.

Already at this simple level, however, one can see how effective complexity and the associated form of integrated information can function as an “objective valuation” in the sense defined by Kantorovich in [18], as opposed to the subjective price valuations of markets. To see an explicit example of how this works, consider one of the “instruments of complexity” mentioned above: the visual arts.

Let’s look at paintings: in a market system the value of art is subject to the vagaries of the art market, whose completely devastating effects on contemporary art, starting in the 1980s, have been discussed at length, [17]. In a cybernetic communism system art is an instrument for growing complexity. Its objective valuation is the effective complexity content. This of course can be evaluated at many levels, starting with the relation of the art work to its contemporary society. However, just to keep the example simple, let’s focus only on what may be regarded as the “aesthetic” level. This is usually the most difficult and subjective aspect to evaluate, but in our setting we are only trying to gauge its effect as a complexity generator. If one studies how paintings in different art movements throughout the history of art are distributed on a plane with coordinates given by Shannon entropy and Kolmogorov complexity (as is done in [32]) one finds an interesting distribution, where artistic movements like Minimalism, Color Field Painting, and Conceptual Art have higher values of Kolmogorov complexity and lower values of Shannon Entropy, others like Lyrical Abstraction, Abstract Expressionism, and Op Art have intermediate values of both, and at the other end Cubism, Tachism, or Pointillism have high Shannon entropy and low Kolmogorov complexity. What is more interesting, though, is that in terms of the total information function (which as recalled earlier is a sum of Shannon entropy and Kolmogorov complexity and is the basis for defining effective complexity) all these different art movements are placed around very similar values, since (as shown in [32]) in the (H; K) entropy-complexity plane they are distributed roughly around a line with constant sum K+H. This supports the idea that visual art (painting in this case) functions as an instrument of complexity with a certain objective capacity for effective complexity generation.

This view of the arts and culture and their crucial role in the dynamics of socialist development is very close to the original grand vision of the anarcho-communist avant-garde in the running up to the Russian Revolution and in the years that immediately followed, before Stalinism wiped it out entirely, [1], [8], [15].

Multilayered Networks

In the modeling of the scaling problem, passing from the small to the large scales happens through connectivity. We are assuming that the problem of anarcho-communism organization is working well on the small scales, which means that we have individual workers-owned cooperatives and other similar initiatives that are running according to anarcho-communist principles. The process of growth to larger scales is based on network structures connecting them. We can assume that the nodes of a network are individual cooperatives, as we do not need a finer resolution to smaller scales. Just thinking of a network of connections is inadequate: what one really needs are multiple interconnected networks that describe different forms of sharing (or different kind of services, of resources, of information). The appropriate kind of model for this type of structures is provided by the theory of multilayered networks, [7]. Not only this makes it possible to describe different networking structures that simultaneously exist, that represent different forms of sharing, but it also allows for a description of how each of these layers changes over time in a dynamical way, in interaction with the other layers. Roughly we should think of each of the different kinds of “instruments” described above as generating its own layer in a multilayered network, with interdependencies with all the other layers.

In general, when one studies large complex networks, which are subject to continuous changes in time, it is better to work with a probabilistic approach and regard the possible networking structures as a statistical mechanical ensemble, where certain general properties of the network are fixed as constraints and one considers probabilities of connections between nodes, either within (infralayer) or across layers (intralayer). Various different models for the growth of networks are possible: in particular, in collaboration networks, which are close to the kind of models we are considering, one usually assumes triadic closures. This means that, when a new node gets connected to an old node, other nodes that are already collaborators of the old nodes (neighbors in the net) are more likely to get connected to the new node as well. Also, some cost functions may be added in the probability of connection: for example, for layers of the network that model physical distribution of services geographic distance is a cost, while for information sharing (provided an infrastructure network like the internet is already accounted for by another layer) geographic distance is irrelevant. This is again an example of the fact that valuations that estimate minimization of costs in the linear programming sense are themselves dependent on the layer of the network and on the scale.

Regarding the more interesting part of the optimization process, the maximization of integrated informational complexity, one can consider a dynamics for the network that generalizes frequently used models of Shannon entropy maximization, [7].

Communities

To implement a form of dynamics based on the optimization of integrated informational complexity on a multilayered network, an important role is played by communities in the network. These are intermediate structures between the individual nodes and the large scale of the entire network.

Communities are a familiar notion in anarchism: they are sometimes conceived in terms of identity, especially in contexts such as decolonization, indigenous cultures, organizations aimed at liberation of oppressed populations. Communities can also form around shared projects and specific initiatives. All of these are of vital importance to the anarchist project. As intersectionality has taught us regarding the understanding of forms of oppression, the notions of identity and community are subtle and their overlapping structure is important. In the case of complex networks there are usually many overlapping communities, some of them easily detectable in the connectivity structure of the network, some more difficult to identify, but significant in terms of determining the scaling properties of the network. The structure of communities (the modularity properties of the network) can be regarded as the important intermediate step between the small scale of individual nodes and their local connectivity and the large scales. There are various algorithmic approaches to the identification of communities in networks, [7]. In the case of multilayered networks, one additionally wants to understand how communities in a layer relate to communities in other layers (whether the structure of communities remains similar, or changes significantly across layers) and also which parts of different layers should be regarded as part of the same communities.

Informational complexity and network communities

An informational measure of proximity in the community structure of different layers of multilayered networks is provided by the normalized mutual information.  Given a community structure with communities σ in the layer L_α and communities σ’   in the layer L_β the normalized mutual information is given by

(7)

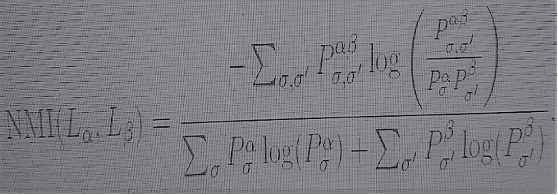
where

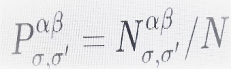
is the fraction of nodes that simultaneously belong to the communities σ  in layer L_α and  σ’   in layer L_β ,

and similarly  and 

are the fractions of nodes in the community σ  in layer L_α, respectively in the community σ’  in layerL_β  . The numerator of (7) is a Kullback-Leibler divergence as in (5), measuring the difference between the community structure of the two joined layers and the one obtained if the two layers were completely independent, while the denominator normalizes it with respect to the total Shannon entropy of the community structures of two layers, seen as independent.

Here the comparison through the Kullback-Leibler divergence of the joint distribution of nodes in communities across the two strata, given by

 

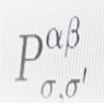
with the one for independent strata, given by the product  

is clearly reminiscent of integrated information (6), and it can indeed be transformed into an integrated information measure by considering all the possible community structures on the network layers, just as one considers all possible partitions of a system in (6). We can then take the further step of replacing entropy with effective complexity and weight the community structures across layers in terms of a normalized relative effective complexity. This will provide a way to define a dynamics of complex networks that implements from small to large scales the optimization of integrated informational complexity, as an alternative to the profit optimization of market models.

Provisional conclusion

Markets are often proposed, also within anarchist settings, as a computational model to address the scale problem. Alternative computational models can be envisioned, which do not rely on profit, but on the optimization of a form of integrated informational complexity. These can provide an alternative to the market system to address the scale problem in an anarcho-communist perspective. The purpose of this note was to outline some of these ideas, while avoiding most of the technicalities involved. It should not be regarded in any way as a complete treatment, as the problem discussed here is very much open and would require much more extensive theoretical elaboration.

June 2020

……………………………………………………………………………….

N.B. The feature image, the photos and their captions on the Aurora Apolito’s text have been added by me, J. Catarino Soares, the webmaster of this site. If required, I will accept the blame for choosing them, and for whatever deficiencies they may contain.

…………………………………………………………………………………

References

[1] Allan Antliff, Anarchist Modernism, University of Chicago Press, 2007.

[2] Nihat Ay, Markus Mueller, Arleta Szkola, Effective complexity and its relation to logical depth, IEEE Trans. Inf. Th., Vol. 56/9 (2010) 4593–4607. [arXiv:0810.5663]

[3] Charles H. Bennett, Logical Depth and Physical Complexity, in “The Universal Turing Machine – a Half-Century Survey” (Ed. Rolf Herken), Oxford University Press, 1988.

 [4] Charles H. Bennett, Peter Gács, Ming Li, Paul M.B. Vitányi, Wojciech H. Zurek, Information distance, IEEE Transactions on Information Theory, 44(1998) N.4, 1407–1423.

 [5] Franco ‘Bifo’ Berardi, The Uprising: On Poetry and Finance, Semiotext(e), 2012.

[6] Franco ‘Bifo’ Berardi, Breathing: Chaos and Poetry, Semiotext(e), 2019.

[7] Ginestra Bianconi, Multilayer Networks, Oxford University Press, 2018.

[8] John E. Bowlt and Olga Matich, eds., Laboratory of Dreams: The Russian Avant-garde and Cultural Experiment, Stanford University Press, 1996.

[9] William Davies (Ed.), Economic Science Fictions, Goldsmiths Press, 2019.

[10] Jean-Paul Delahaye, Complexité aléatoire et complexité organisée, Editions Quae, 2009.

[11] Murray Gell-Mann, What is Complexity? Complexity, Vol.1 (1995) N.1 [9 pages].

[12] Murray Gell-Mann, Seth Lloyd, Information Measures, Effective Complexity, and Total Information, Complexity, Vol. 2 (1996) 44–52.

[13] Slava Gerovitch, From Newspeak to Cyberspeak. A History of Soviet Cybernetics, MIT Press, 2002.

 [14] George Gorelik, Bogdanov’s Tektology, General Systems Theory, and Cybernetics, Hemisphere Publishing, 1987.

 [15] Nina Gourianova, The Aesthetics of Anarchy: Art and Ideology in the Early Russian Avant-Garde, University of California Press, 2012.

[16] Simon Ings, Stalin and the Scientists: A History of Triumph and Tragedy, 1905–1953, Open Road & Grove Atlantic, 2017.

[17] Annamma Joy, John F. Sherry, Jr., Disentangling the paradoxical alliances between art market and art world, Consumption, Markets & Culture, Vol.6 (2003), N.3, 155–181.

[18] Leonid Vitaliyevich Kantorovich, Mathematical methods of organization and planning of production, Leningrad State University Press, 1939.

[19] Anatoly Kitov, Aleksei Lyapunov, Sergei Sobolev, The Main Features of Cybernetics, Voprosy filosofii (Problems of Philosophy), No. 4 (1955), 136–148.

[20] Christoph Koch, The feeling of life itself, MIT Press, 2019.

[21] Nikolai Krementsov, A Martian Stranded on Earth: Alexander Bogdanov, Blood Transfusions, and Proletarian Science, The University of Chicago Press, 2011.

[22] David A. Lax, Libermanism and the Kosygin reform, University of Virginia Press, 1991.

[23] Ming Li, Paul Vitányi, An Introduction to Kolmogorov Complexity and Its Applications, Springer, 1997 [New Edition, 2008].

[24] Evsei G. Liberman, Plans, Profits, and Bonuses, Pravda, September 9, 1962.

[25] Marcello Massimini, Giulio Tononi, Sizing up consciousness, Oxford University Press, 2018.

[26] Warren S. McCulloch, A Heterarchy of Values Determines by the Topology of Nervous Nets, Bulletin of Mathematical Biophysics, 7 (1945) 89–93.

[27] Eden Medina, Cybernetic Revolutionaries. Technology and Politics in Allende’s Chile, MIT Press, 2011.

[28] Benjamin Peters, How Not to Network a Nation. The Uneasy History of the Soviet Internet, MIT Press, 2016.

[29] Ethan Pollock, Stalin and the Soviet Science Wars, Princeton University Press, 2006.

 [30] M. Oizumi, N. Tsuchiya, S. Amari, Unified framework for information integration based on information geometry, PNAS, Vol. 113 (2016) N. 51, 14817–14822.

[31] Jaeweon Shin, Michael Holton Price, David H. Wolpert, Hajime Shimao, Brendan Tracey, Timothy A. Kohler, Scale and information-processing thresholds in Holocene social evolution, Nature Communications (2020) 11:2394 https://doi.org/10.1038/s41467-020-16035-9

 [32] Higor Y. D. Sigaki, Matjaž Perc, Haroldo V. Ribeiro, History of art paintings through the lens of entropy and complexity, PNAS, Vol.115 (2018) N.37, E8585–E8594

 [33] G. Tononi G (2008) Consciousness as integrated information: A provisional manifesto, Biol. Bull. 215 (2008) N.3, 216–242.

[34] Anatoly Vershik, L.V.Kantorovich and Linear Programming, arXiv:0707.0491.

[35] Norbert Wiener, Cybernetics, or control and communication in the animal and the machine, MIT Press, 1948.

……………………………………………………………………………..

[*] Aurora Apolito is a mathematician and theoretical physicist. She also works on linguistics and neuroscience. She studied physics in Italy and mathematics in the US, and worked for various scientific institutions in the US, Canada, and Germany.  Aurora Apolito is a pen name meant to differentiate her research in political philosophy from her work in other fields.